题目内容
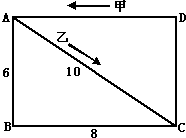 如图(单位:千米),长方形ABCD的四个顶点均为汽车停靠站,甲车A-B-C-D-A-B-…逆时针行驶,速度为60千米/小时;乙车沿A-C-D-A-C-…逆时针行驶,速度为30千米/小时.两车每到一个站都停留2分钟.两车同时从A站出发后,第一次在A站相遇最小需多长时间?
如图(单位:千米),长方形ABCD的四个顶点均为汽车停靠站,甲车A-B-C-D-A-B-…逆时针行驶,速度为60千米/小时;乙车沿A-C-D-A-C-…逆时针行驶,速度为30千米/小时.两车每到一个站都停留2分钟.两车同时从A站出发后,第一次在A站相遇最小需多长时间?分析:甲车A-B-C-D-A-B-…逆时针行驶,速度为60千米/小时,就是每分钟走1千米,乙车沿A-C-D-A-C-…逆时针行驶,速度为30千米/小时,就是每分钟走0.5千米,分别求出两车回到A点走的路程,从而求出走的时间,再加上停留的时间就是两车再次出发的时间,在A站相遇最小时间是两车再次出发时间的最小公倍数减去停留的2分钟,据此计算即可解答.
解答:解:甲车每分钟走1千米,相邻两次离开A站相隔(8+6+8+6)÷1+2×4=36分钟,
乙车每分钟走0.5千米,相邻两次离开A站相隔(8+6+10)÷0.5+2×3=54分钟,
36和54的最小公倍数是108,
108-2=106(分钟)
答:出发106分钟后,两车第一次在A点相遇.
乙车每分钟走0.5千米,相邻两次离开A站相隔(8+6+10)÷0.5+2×3=54分钟,
36和54的最小公倍数是108,
108-2=106(分钟)
答:出发106分钟后,两车第一次在A点相遇.
点评:本题主要考查相遇问题,求出两车回到A点经过的时间是解答本题的关键.

练习册系列答案
相关题目


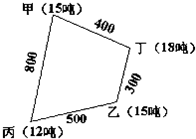 如图,甲、乙两个工厂各需15吨钢材,而丙、丁两个仓库分别有12吨、18吨钢材,每吨钢材运1千米的运费相同.问:如何调运能使运费最省?(工厂与仓库之间的路程见图,单位:千米)
如图,甲、乙两个工厂各需15吨钢材,而丙、丁两个仓库分别有12吨、18吨钢材,每吨钢材运1千米的运费相同.问:如何调运能使运费最省?(工厂与仓库之间的路程见图,单位:千米) 如图(单位:千米),长方形ABCD的四个顶点均为汽车停靠站,甲车A-B-C-D-A-B-…逆时针行驶,速度为60千米/小时;乙车沿A-C-D-A-C-…逆时针行驶,速度为30千米/小时.两车每到一个站都停留2分钟.两车同时从A站出发后,第一次在A站相遇最小需多长时间?
如图(单位:千米),长方形ABCD的四个顶点均为汽车停靠站,甲车A-B-C-D-A-B-…逆时针行驶,速度为60千米/小时;乙车沿A-C-D-A-C-…逆时针行驶,速度为30千米/小时.两车每到一个站都停留2分钟.两车同时从A站出发后,第一次在A站相遇最小需多长时间?