题目内容
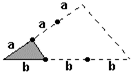
如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的________倍.
9
分析:因大三角形的两条边分别被三等分,根据:如果三角形的高相等,则高所在边的长度比就等于面积比,可以求得结果.
解答:分别连接由b边延长得到的等分点与对应的顶点,则得到三个一b为底边的三个面积相等的三角形,又因最左边的面积与阴影的面积比是3:1,所以阴影的面积与大三角形的面积比是1:9,则这个大三角形的面积是原三角形面积的9倍.
故此题应填9.
点评:此题主要考查等底等高的三角形面积相等.
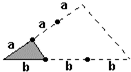
分析:因大三角形的两条边分别被三等分,根据:如果三角形的高相等,则高所在边的长度比就等于面积比,可以求得结果.
解答:分别连接由b边延长得到的等分点与对应的顶点,则得到三个一b为底边的三个面积相等的三角形,又因最左边的面积与阴影的面积比是3:1,所以阴影的面积与大三角形的面积比是1:9,则这个大三角形的面积是原三角形面积的9倍.
故此题应填9.
点评:此题主要考查等底等高的三角形面积相等.

练习册系列答案
相关题目