题目内容
【题目】下图是一个平行四边形，BE：EC=1：2，F是DC的中点，三角形ABE的面积是6cm2，那么三角形ADF的面积是________cm2。
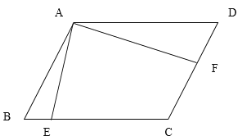
【答案】9
【解析】
根据题意，先连接AC，则三角形ADF的面积就是三角形ACD的一半，由此只要求出三角形ACD的面积即可，因为三角形ACD与三角形ABC的面积相等，都等于平行四边形面积的一半，这里只要利用BE：EC=1：2，可以得出BC=3BE，再利用高一定时，三角形的面积与底成正比例，计算出三角形ABC的面积，也是三角形ADC的面积，然后除以2即可得到三角形ADF的面积，据此列式解答.
根据分析，作图如下：
，
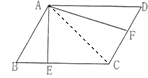因为BE：EC=1：2，所以BC=3BE，又因为三角形ABE的面积是6平方厘米，
所以三角形ABC的面积为：6×3=18（平方厘米），则三角形ACD的面积是18平方厘米；
因为F是CD的中点，
所以三角形ADF的面积为：18÷2=9（平方厘米）.
故答案为：9.
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
