题目内容
7．
用
在月历卡上任意框出5个数（如图1）（1）如果用a表示正中间的数，请在框中表示出其余4个数
（2）能框出和是60的5个数吗？为什么？
（3）一共能框出多少个不同的和？
分析 （1）如果用a表示正中间的数，那么它左边的数为a-1，右边的数为a+1，上边的数为a-7，下边的数为a+7．
（2）从表中看出，框出的五个数中，两边的两个数的和是中间的数的2倍，据此解答问题即可．
（3）因为第一行、第二行和第三行可以框出4个的和；第二行、第三行与第四行可以框出5个不同的和，第三行、第四行与第五行可以框出4个不同的和，因此即可得出一共框出的不同的和的个数．
解答 解：（1）如果用a表示正中间的数，请在图2框中表示出其余4个数，答案如图：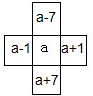
（2）根据第一问可知，框出的五个数的和是中间数的5倍，
60÷5=12
所以最中间的数是12
如图：
答：不能．和是60最中间的数是12，而图中这五个数不是这样排列的．
（3）因为第一行、第二行和第三行可以框出4个的和；第二行、第三行与第四行可以框出5个不同的和，第三行、第四行与第五行可以框出4个不同的和，因此即可得出一共框出的不同的和的个数．
所以一共框出的不同的和的个数：4+5+4=13．
答：共框出13个不同的和．
点评 考查了简单图形覆盖现象中的规律，解答此题的关键是，根据所给出的阴影部分的数与数的关系，得出规律，再根据规律解决问题．
练习册系列答案
名校课堂系列答案
相关题目
如图，如果用A（2，1）表示放置2个胡萝卜，1棵白菜；点B（4，2）表示放置4个胡萝卜，2棵白菜：
19．
| 脱式计算．（能简便的要简便计算） ①$\frac{2}{3}$+（$\frac{5}{6}$-$\frac{3}{4}$）÷$\frac{3}{8}$ | ②360÷15-2.5×1.4 | ③$\frac{3}{7}$-$\frac{2}{5}$+$\frac{4}{7}$-$\frac{3}{5}$ |
| ④43×99+43 | ⑤（$\frac{1}{15}$+$\frac{2}{17}$）×15×17 | ⑥99×22+33×34． |