题目内容
14.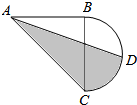 三角形ABC是等腰直角三角形.以BC为直径,BC中点O为圆心画半圆,D为半圆周的中点,连结AD,已知AB=BC=10厘米,求阴影部分的面积.
三角形ABC是等腰直角三角形.以BC为直径,BC中点O为圆心画半圆,D为半圆周的中点,连结AD,已知AB=BC=10厘米,求阴影部分的面积.
分析 先作辅助线,即可得出:空白部分的面积为三角形AED的面积减去正方形BEDO的面积再加上圆面积的$\frac{1}{4}$,将数据代入公式即可求解;而这个图形的面积为等腰直角三角形的面积和半圆的面积之和,用这个图形的面积减去空白部分的面积,即可得解.
解答 解:如图作出辅助线: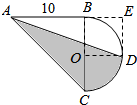
则空白部分的面积为三角形AED的面积减去正方形BEDO的面积再加上圆面积的$\frac{1}{4}$.
三角形AED的面积是(10+10÷2)×(10÷2)×$\frac{1}{2}$;
正方形面积是(10÷2)2,
圆面积的$\frac{1}{4}$是$\frac{1}{4}$×3.14×(10÷2)2,
故空白部分面积为:(10+10÷2)×(10÷2)×$\frac{1}{2}$-(10÷2)2+$\frac{1}{4}$×3.14×(10÷2)2
=37.5-25+19.625
=32.125(平方厘米).
所以阴影部分的面积为:
10×10÷2+3.14×(10÷2)2÷2-32.125
=50+39.25-32125
=57.125(平方厘米)
答:阴影部分的面积是57.125平方厘米
点评 解决此题的关键是做出合适的辅助线,将图形进行相应转换,利用已知条件求得阴影部分的面积.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
11.一堆煤,用去$\frac{3}{5}$,用去与剩下的比是( )
| A. | 3:5 | B. | 2:5 | C. | 3:2 | D. | 2:3 |
5.根据统计表,完成统计图,并回答问题.
李叔叔的文具店今年前5个月的经营情况如下表:
(1)根据表中的信息画出折线统计图
李叔叔的文具店1-5月的经营与支出情况统计图:
(2)根据以上信息回答问题:
A、1-5月份营业额的变化趋势是怎样的?
B、哪个月的营业额最高?
C、你还能提出什么问题?
李叔叔的文具店今年前5个月的经营情况如下表:
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 营业额(万元) | 3 | 3.5 | 3.8 | 4 | 5 |
| 支出(万元) | 2.5 | 2.8 | 3 | 3.5 | 4 |
李叔叔的文具店1-5月的经营与支出情况统计图:
(2)根据以上信息回答问题:
A、1-5月份营业额的变化趋势是怎样的?
B、哪个月的营业额最高?
C、你还能提出什么问题?
2.用体积是1立方厘米的小正方体拼成一个比它大的正方体,至少要( )个才能拼成.
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |