Question

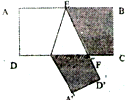如图，在长方形ABCD中，AB=12cm，BC=6cm，当E、F分别在AB、CD上，将长方形ABCD沿着EF折叠，使B、C分别落在长方形外部B、C，则整个阴影部分的周长是为

1. A.
   16
2. B.
   18
3. C.
   20
4. D.
   36

Answer 1

D
分析：将长方形ABCD沿着EF折叠后，线段AD移到了A′D′，线段DG移到了GA′，线段AE移到了ED′；整个阴影部分的周长=（ED′+EB）+BC+（GC+GA′）+A′D′=AB+BC+DC+AD=长方形ABCD的周长；所以求整个阴影部分的周长就等于求长方形ABCD的周长．

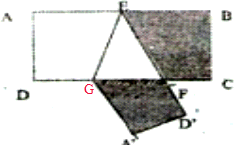
解答：根据分析可得：
（12+6）×2，
=18×2，
=36（cm）；
答：整个阴影部分的周长是为36cm．
故选：D．
点评：本题考查了简单图形的折叠问题，这类问题要抓住折叠后原来部分的面积和边的长度不变，只是移动了位置．