题目内容
19.2014盏灯排成一排,开始都亮着,第一次从左边第一盏开始,每隔一盏灯拉一下开关(即拉左数1、3、5、…2014盏);第二次从右边第一盏开始每隔两盏拉一下开关;第三次从左边第一盏开始,每隔3盏拉一下开关,此时亮着的还有1172盏.分析 第一次拉开关,所有编号为奇数的灯被拉一次,第二次拉开关,所有编号能被3整除的灯被拉了一次,第三次拉开关,所有编号为“被4除余1的数”的灯被拉了一次,这样就会得出一个规律,先求出2、3、4的最小公倍数为12,然后分析从1到12号灯三轮过后的亮灭情况,因为每12盏灯的情况为一个周期,被拉过三次的有只有9号,被拉过两次的有(1、3、5)号三盏,被拉过一次的有(6、7、11、12)四盏,剩下的四盏没有被拉过.因为灯被拉过偶数次(0是偶数)就会亮着,所以有3+4=7盏灯亮着.从13号到24号情况和1到12是一样的.接下来2014÷12=167(个周期)…10(个号)剩下的10个号亮灭情况跟1到12号是一样的.所以,这6盏灯里面没有被拉过三次的,其中只有2010号灯被拉过1次,其他5盏都被拉过偶数次,所以这10盏灯有3盏亮着.三次都拉到的灯有167盏;亮着的灯有167×7+3=1172盏.
解答 解:由分析知:
先求出2、3、4的最小公倍数为12,
然后分析从1到12号灯三轮过后的亮灭情况,因为每12盏灯的情况为一个周期,被拉过三次的有只有9号,被拉过两次的有(1、3、5)号三盏,被拉过一次的有(6、7、11、12)四盏,剩下的四盏没有被拉过,
因为灯被拉过偶数次(0是偶数)就会亮着,所以有3+4=7盏灯亮着,
来2014÷12=167(个周期)…10(个号),剩下的10个号亮灭情况跟1到12号是一样的,
所以,这10盏灯里面没有被拉过三次的,所以这10盏灯有3盏亮着,
亮着的灯有167×7+3=1172盏;
故答案为:1172.
点评 此题主要考查了整数的整除性问题,解题时根据数的整除,首先分别求出2、3、4的最小公倍数,1到12号灯三轮过后的亮灭情况是一个周期,然后进行解答即可.

| A. | 140元 | B. | 240元 | C. | 260元 | D. | 300元 |
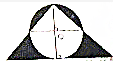 如图,圆的直径是12cm,等腰直角三角形的底边长是24cm,求阴影部分的面积.
如图,圆的直径是12cm,等腰直角三角形的底边长是24cm,求阴影部分的面积. 一个底面是正方形的长方体纸盒,它的展开图如图,这个长方体的体积是多少立方厘米?
一个底面是正方形的长方体纸盒,它的展开图如图,这个长方体的体积是多少立方厘米?