题目内容
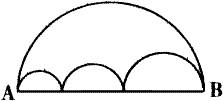
如图，小圆和大圆的半径的比是________．直径的比是________，周长的比是________，面积的比是________．
1：2 1：2 1：2 1：4
分析：设小圆的半径是r，则小圆的直径是2r，大圆的半径是2r，（1）进而求出小圆半径和大圆半径的比；（2）根据“圆的直径=2r”求出小圆和大圆的直径，然后进行比即可；（3）根据“圆的周长=2πr”分别计算出小圆和大圆的周长，然后进行比即可；（4）根据“圆的面积=πr2”分别计算出小圆和大圆的面积，然后进行比即可．
解答：设小圆的半径是r，则小圆的直径是2r，大圆的半径是2r，则：
（1）r：2r=1：2；
（2）（2r）：（2r×2）=1：2；
（3）（2πr））：[2×π×（2r）]，
=2πr：4πr，
=1：2；
（4）πr2：π（2r）2，
=πr2：4πr2，
=1：4；
故答案为：1：2，1：2，1：2，1：4．
点评：解答此题的关键：先假设出小圆和大圆的半径，进而结合题意，根据直径和半径之间的关系，圆的周长的计算方法和圆的面积的计算方法进行解答，继而得出结论．
分析：设小圆的半径是r，则小圆的直径是2r，大圆的半径是2r，（1）进而求出小圆半径和大圆半径的比；（2）根据“圆的直径=2r”求出小圆和大圆的直径，然后进行比即可；（3）根据“圆的周长=2πr”分别计算出小圆和大圆的周长，然后进行比即可；（4）根据“圆的面积=πr2”分别计算出小圆和大圆的面积，然后进行比即可．
解答：设小圆的半径是r，则小圆的直径是2r，大圆的半径是2r，则：
（1）r：2r=1：2；
（2）（2r）：（2r×2）=1：2；
（3）（2πr））：[2×π×（2r）]，
=2πr：4πr，
=1：2；
（4）πr2：π（2r）2，
=πr2：4πr2，
=1：4；
故答案为：1：2，1：2，1：2，1：4．
点评：解答此题的关键：先假设出小圆和大圆的半径，进而结合题意，根据直径和半径之间的关系，圆的周长的计算方法和圆的面积的计算方法进行解答，继而得出结论．
练习册系列答案
相关题目
