Question

【题目】75．如图所示，大正方形的面积比小正方形的面积多1O平方厘米．求两正方形之间的圆面积．

Answer 1

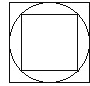
【答案】5.7平方厘米

【解析】

试题分析：由图意可知：大正方形的面积﹣正方形的面积=10，这个最大圆的直径应该等于小正方形的对角线的长度，最大圆的直径等于大正方形的边长，可设圆的半径为r，然后计算出大正方形和小正方形各自的面积，从而可以计算出圆的半径的平方，两正方形之间圆的面积等于圆的面积减去小正方形的面积，列式解答即可得到答案．

解：

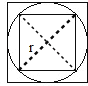
设圆的半径为r，

则大正方形的面积为：2r×2r=4r2（平方厘米），

小正方形的面积为：2r×r÷2×2=2r2（平方厘米），

圆的半径为：

4r2﹣2r2=10，

2r2=10，

r2=5，

两正方形之间圆的面积为：

πr2﹣2r2

=3.14×5﹣2×5，

=15.7﹣10，

=5.7（平方厘米），

答：两正方形之间圆的面积是5.7平方厘米．