题目内容
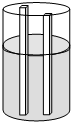 如图两根铁棒直立于桶底水平的木桶中,在桶中加水之后,一根露出水面的长度是它的
如图两根铁棒直立于桶底水平的木桶中,在桶中加水之后,一根露出水面的长度是它的| 1 |
| 3 |
| 1 |
| 5 |
分析:由于没入水中长度是一样的,设水深为x厘米,则第一根的长度为x÷(1-
),第二根的长度为x÷( 1-
),由此可得方程:x÷(1-
)+x÷( 1-
)=55,解此方程即可.
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
解答:解:,设水深为x厘米,可得方程:
x÷(1-
)+x÷( 1-
)=55,
x÷
+x÷
=55,
x+
x=55,
(
+
)x=55,
x=55,
x=20.
答:水深20厘米.
x÷(1-
| 1 |
| 3 |
| 1 |
| 5 |
x÷
| 2 |
| 3 |
| 4 |
| 5 |
| 3 |
| 2 |
| 5 |
| 4 |
(
| 3 |
| 2 |
| 5 |
| 4 |
| 11 |
| 4 |
x=20.
答:水深20厘米.
点评:明确没入水中的长度即是水深,并由此设未知数列出方程是完成本题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2012?湖北)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根铁棒在水面以上的长度是总长的
(2012?湖北)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根铁棒在水面以上的长度是总长的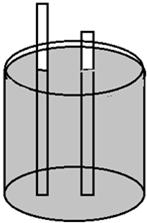 (2013?龙海市模拟)如图,两根铁棒直立于桶底水平的桶中,在桶中加入水后,一根铁棒在水面以上的长度是总长的
(2013?龙海市模拟)如图,两根铁棒直立于桶底水平的桶中,在桶中加入水后,一根铁棒在水面以上的长度是总长的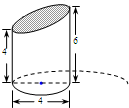 如图,是一个直立于水平面上的几何体(它是圆柱的一部分,下底面为圆面,单位:cm).则这个几何体的体积为
如图,是一个直立于水平面上的几何体(它是圆柱的一部分,下底面为圆面,单位:cm).则这个几何体的体积为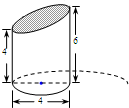 如图,是一个直立于水平面上的几何体(它是圆柱的一部分,下底面为圆面,单位:cm).则这个几何体的体积为________cm3.(计算结果保留π)
如图,是一个直立于水平面上的几何体(它是圆柱的一部分,下底面为圆面,单位:cm).则这个几何体的体积为________cm3.(计算结果保留π)