题目内容
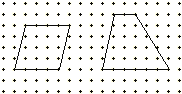
【题目】如图，长方形ABCD中有两条平行线，将它分成了一个梯形AEGB、平行四边形EFCG和三角形FDC。AE：EF：FD=2：1：2，那么梯形、平行四边形、三角形面积的比是________。
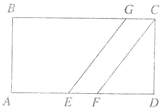
【答案】3：1：1
【解析】
长方形的对边相等，根据条件“ AE：EF：FD=2：1：2 ”可知，把AE看作2份，EF看作1份，FD看作2份，求出BG的长度，然后设长方形的宽是h，则梯形AEGB、平行四边形EFCG、三角形FDC的高也是h，依据梯形的面积=（上底+下底）×高÷2，平行四边形的面积=底×高，三角形的面积=底×高÷2，写出它们的面积，然后化简它们的面积比，据此解答.
BG=AE+DF=2+2=4；
设长方形的宽是h，则梯形AEGB、平行四边形EFCG、三角形FDC的高也是h，
梯形、平行四边形、三角形面积的比是：
（2+4）×h÷2：1×h：2×h÷2
=6h÷2：h：h
=3h：h：h
=3：1：1.
故答案为：3：1：1.
练习册系列答案
相关题目
【题目】根据表中的数据，在下图中描出相应的点，并把它们用线连起来
路程/千米 | 时间/时 |
30 | 1 |
60 | 2 |
90 | 3 |
120 | 4 |
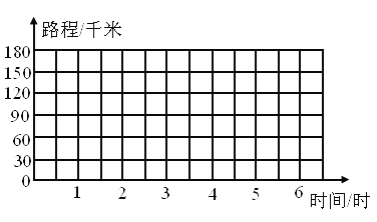
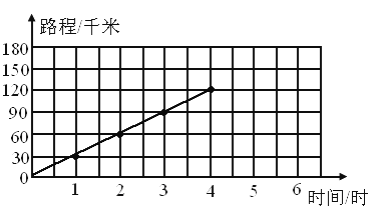
（1）路程和时间成比例吗？________(填成或不成)成什么比例？________(填正比例、反比例或不成比例)
（2）根据图像判断，这辆汽车行驶150千米需要________小时？6小时能行驶________千米？
（3）根据表格中的数据，在图中描出相应的点，并把它们用线连起来.
