题目内容
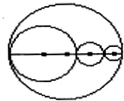 在如图中,四个圆的圆心在一条直线上,大圈的周长与三个小圆的周长之和比较,结果是
在如图中,四个圆的圆心在一条直线上,大圈的周长与三个小圆的周长之和比较,结果是
- A.大于
- B.小于
- C.等于
C
分析:设大圆的直径为d,三个小圆的直径分别为d1、d2、d3,则大圆的周长为πd,三个小圆的周长和为πd1+πd2+πd3=(d1+d2+d3)π,又d1+d2+d3=d,所以,πd=πd1+πd2+πd3.
解答:设大圆的直径为d,三个小圆的直径分别为d1、d2、d3,
则:πd1+πd2+πd3=(d1+d2+d3)π,
又d1+d2+d3=d,
所以,πd=πd1+πd2+π,即大圆的周长与三个小圆的周长相等.
故选:C.
点评:完成本题关键是据圆的周长公式进行推理.
分析:设大圆的直径为d,三个小圆的直径分别为d1、d2、d3,则大圆的周长为πd,三个小圆的周长和为πd1+πd2+πd3=(d1+d2+d3)π,又d1+d2+d3=d,所以,πd=πd1+πd2+πd3.
解答:设大圆的直径为d,三个小圆的直径分别为d1、d2、d3,
则:πd1+πd2+πd3=(d1+d2+d3)π,
又d1+d2+d3=d,
所以,πd=πd1+πd2+π,即大圆的周长与三个小圆的周长相等.
故选:C.
点评:完成本题关键是据圆的周长公式进行推理.

练习册系列答案
相关题目
 (1)作为上海经济发展的“助推器”和上海中心城区的“辅城”--临港新城,将在南汇崛起.据规划,临港新城总面积达297平方公里,分四个功能区:主城区、主产业区、重装备产业区和物流园区、综合区.部分规划数据见下表.请根据所提供的数据完成下列问题(结果精确到个位).
(1)作为上海经济发展的“助推器”和上海中心城区的“辅城”--临港新城,将在南汇崛起.据规划,临港新城总面积达297平方公里,分四个功能区:主城区、主产业区、重装备产业区和物流园区、综合区.部分规划数据见下表.请根据所提供的数据完成下列问题(结果精确到个位).
| 规划面积 (单位:平方公里) | 占临港新城规划总面积的百分比 | |
| 主城区 | ||
| 主产业区 | 102 | |
| 重装备产业区和物流园区 | 79 | |
| 综合区 | 14% |
②如果南汇全区总面积688平方公里,那么临港新城占全区总面积的百分比是多少?
(2)如图,正方形的边长为8cm,一个半径为1cm的圆沿着正方形的四边内侧滚动一周,求圆滚过的面积.
 在如图中,四个圆的圆心在一条直线上,大圈的周长与三个小圆的周长之和比较,结果是( )
在如图中,四个圆的圆心在一条直线上,大圈的周长与三个小圆的周长之和比较,结果是( ) 如图,四个圆相互交叉,它们把四个圆面分成13个区域.如果在这些区域上(加点的)分别填上6至18的自然数,然后把每个圆中的数各自分别相加,最后把这四个圆的和相加得总和,那么总和最大可能是多少?
如图,四个圆相互交叉,它们把四个圆面分成13个区域.如果在这些区域上(加点的)分别填上6至18的自然数,然后把每个圆中的数各自分别相加,最后把这四个圆的和相加得总和,那么总和最大可能是多少?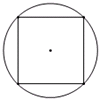 如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:
如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为: