题目内容
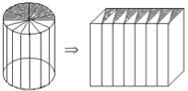
【题目】（4分）如图：把一个圆柱体沿高切成底面是若干相等的底面是扇形的几何体，再拼成一个近似长方体．若拼成的长方体前面与右侧面的面积和是207平方厘米，且原来圆柱高是5厘米，则原来圆柱的体积是多少立方厘米？
【答案】答：原来圆柱的体积是1570立方厘米
【解析】
试题分析：设圆柱底面半径为r厘米，因为拼成的长方体前面与右侧面的面积之和就是圆柱侧面积的一半和圆柱的高与半径的积的和，由此可得方程：2×3.14×r×5÷2+5r=207，解方程求出r，进而根据：圆柱的体积=πr2h，由此解答即可．
解：设圆柱底面半径为r厘米，则：
2×3.14×r×5÷2+5r=207
15.7r+5r=207
20.7r=207
r=10
原来圆柱的体积为：
3.14×102×5=1570（平方厘米）
答：原来圆柱的体积是1570立方厘米．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
