题目内容
 如图,已知大正方形的周长是48厘米,AD:DB=1:2,其中一个小三角形的面积是
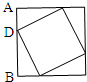
如图,已知大正方形的周长是48厘米,AD:DB=1:2,其中一个小三角形的面积是16
16
平方厘米,小正方形的面积是80
80
平方厘米.分析:先利用正方形的周长公式求出大正方形的边长,进而依据“AD:DB=1:2”,利用按比例分配的方法,即可求出AD、DB的长度,也就等于知道了小三角形的两条直角边的长度,从而利用三角形的面积公式即可求出每个小三角形的面积;小正方形的面积=大正方形的面积-三角形的面积×4,代入数据即可求解.
解答:解:大正方形的边长:48÷4=12(厘米),
AD的长度为12×
=4(厘米),
DB的长度为12×
=8(厘米),
其中一个小三角形的面积是:4×8÷2=16(平方厘米);
小正方形的面积是:12×12-16×4,
=144-64,
=80(平方厘米);
答:其中一个小三角形的面积是16平方厘米,小正方形的面积是80平方厘米.
故答案为:16、80.
AD的长度为12×
| 1 |
| 1+2 |
DB的长度为12×
| 2 |
| 1+2 |
其中一个小三角形的面积是:4×8÷2=16(平方厘米);
小正方形的面积是:12×12-16×4,
=144-64,
=80(平方厘米);
答:其中一个小三角形的面积是16平方厘米,小正方形的面积是80平方厘米.
故答案为:16、80.
点评:求出大正方形的边长,进而得出每个小三角形的两条直角边的长度,是解答本题的关键.

练习册系列答案
相关题目
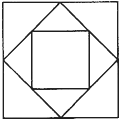
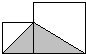 (2012?仙游县模拟)如图,已知大正方形的边长是a厘米,小正方形的边长是b厘米.用字母表示阴影部分的面积是
(2012?仙游县模拟)如图,已知大正方形的边长是a厘米,小正方形的边长是b厘米.用字母表示阴影部分的面积是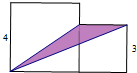 如图,已知大正方形的边长为4,小正方形的边长为3,那么阴影部分的面积为
如图,已知大正方形的边长为4,小正方形的边长为3,那么阴影部分的面积为 如图,已知大正方形的面积比小正方形多52平方分米,大正方形比小正方形的边长多2分米.小正方形的面积是多少?大正方形的面积是多少?
如图,已知大正方形的面积比小正方形多52平方分米,大正方形比小正方形的边长多2分米.小正方形的面积是多少?大正方形的面积是多少?