Question

图形计算：
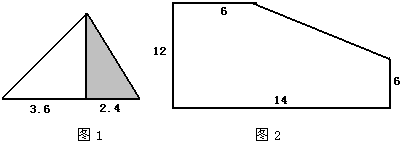
（1）已知图1中两个正方形的边长分别是8厘米和6厘米，求CE的长．
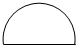
（2）如图2，O是圆心，圆的周长是75.36分米，OABC是梯形，面积是98.28平方分米，AB=20.76分米，那么阴影部分的面积是多少平方分米？（π取3.14）

Answer 1

分析：（1）根据正方形的特点，知道EC平行AB，所以三角形ECD相似与三角形ABD，由此得出对应边的比相等，即可求出CE的长度；
（2）根据圆的周长公式C=2πr，知道r=C÷2π，由此求出OC的长度，再根据梯形的面积公式S=（a+b）×h÷2，知道h=2S÷（a+b），而梯形的高就是三角形AOC的高，所以根据三角形的面积公式即可求出阴影部分的面积．

解答：解：（1）因为三角形ECD相似三角形ABD，所以EC：AB=DC：BD，
所以AB×DC=EC×BD，
即8×6=EC×（8+6），
48=14EC，
EC=48÷14，
EC=

24

7

，

（2）OC=75.36÷3.14÷2=12（分米），
98.28×2÷（12+20.76），
=196.56÷32.76，
=6（分米），
阴影部分的面积：12×6÷2=36（平方分米），
答：CE的长是

24

7

厘米；阴影部分的面积是36平方分米．

点评：（1）关键利用相似三角形的对应边的比相等，列出比例，解答即可；（2）关键是灵活利用圆的周长公式与梯形的面积公式求出梯形的高，即阴影部分的高，再利用三角形的面积公式解决问题．