题目内容
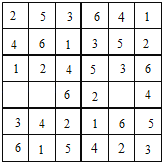
【题目】如图为6×6的数独游戏,在36方格的大宫格内,每行和每列分别填上1至6的数字.大宫格内有 6个分别由6个小方格组成小宫格,以粗线作为分隔.每个小宫格内亦分别填上1至6的数字,请在空白的小格中填上1至6的数字,使得最后每行、每列、每小宫格都不出现重复的数字.
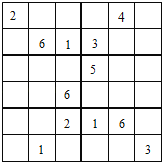
【答案】
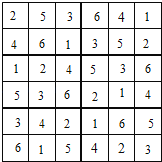
【解析】
试题分析:粗线把这个数独分成了6块,为了便于解答,对各部分进行编号:甲、乙、丙、丁、戊、己,先从各部分中数字最多的己出发,找出其各个小方格里面的数,再根据每行、每列、每小宫格都不出现重复的数字进行推算.
解答:解:对各个小宫格编号如下:
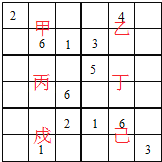
先看己:已经有了数字1、3、6,缺少2、4、5;观察发现:5不能在第四列,4不能在第五列,而2不能在第五行;所以2只能在第六行第五列,4就在第六行第四列,5在第五行第七列;如下:
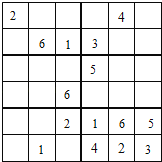
观察上图发现:第四列已经有数字1、3、4、5,缺少2和6,由于2不能在第一行,所以6在第四列的第一行,那么2在第四列的第四行;如下:
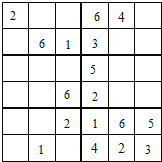
再看乙部分:已经有了数字3、4、6,缺少数字1、2、5,观察上图发现:5不能在第六列,所以5在第五列的第二行;1不能在第二行,所以1至你呢个在第一行的第六列,剩下的2在第二行第六列;如下:

观察上图可知:第二行缺少4,所以第二行第一列是4;第六列缺少4、6,由于6不能在第四行,所以第六列的第三行是6,那么第四行就是4;
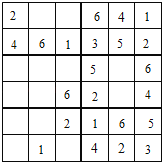
第三列已经有了数字1、2、6,缺少3、4、5,4不能在第一行和第六行,所以第三列的第三行是4,3不能在第六行,所以第三列的第六行是5,那么剩下的3在第三列的第一行;如下:
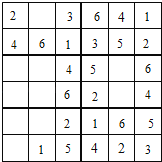
再观察甲部分:已经有了数字1、2、3、4、6,缺少5,所以第一行的第二列就是5;第六行的缺少数字6,所以第六行的第一列就是数字6;

戊部分:已经有了数字1、2、5、6,缺少数字3、4,4不能在第一列,所以第一列的第五行只能是3,第二列的第五行就是4;
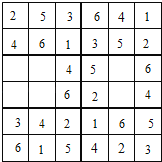
第三行已经有了数字4、5、6,缺少1、2、3;第一列有了数字2、3,所以第三行的第一列就是数字1;第五列有了数字2,所以第三行第五列就是3,剩下的2在第三行第二列;
丁部分缺少数字1,丙部分缺少数字3、5,3不能在第一列,所以第四行第一列是5,第二列是3;那么这个数独就是:


