题目内容
在一条直线上依次有A、B、C、D、E、F 6个点，且相邻两个点间的距离相等，下面能组成比例的是（ ）
分析：根据题意，可知AB=BC=CD=DE=EF，把每一段的距离看作1份数，那么两段就看作2份数，三段就看作3份数，四段就看作4份数，进而写出比例，再看两内项之积是否等于两外项之积，从而确定能否组成比例．
解答：解：见下图：
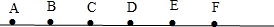
A、1：3和1：2，因为1×2≠1×3，所以不能组成比例；
B、1：2和1：3，因为1×3≠1×2，所以不能组成比例；
C、3：2和3：2，因为3×2=2×3，所以能组成比例；
D、4：2和4：3，因为4×3≠2×4，所以不能组成比例．
故选：C．
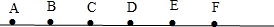
A、1：3和1：2，因为1×2≠1×3，所以不能组成比例；
B、1：2和1：3，因为1×3≠1×2，所以不能组成比例；
C、3：2和3：2，因为3×2=2×3，所以能组成比例；
D、4：2和4：3，因为4×3≠2×4，所以不能组成比例．
故选：C．
点评：解决此题关键是把相邻两个点之间的距离看作1份数，进而根据比例的性质解答．
练习册系列答案
相关题目
