题目内容
【题目】已知实数x、y满足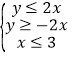
(1)求不等式组表示的平面区域的面积;
(2)若目标函数为z=x-2y,求z的最小值.
【答案】(1)18(2)-9.
【解析】
(1)分别作出约束条件中三条直线的图象,利用三角形面积公式求出所围成的三角形面积即可;(2) 化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论.
画出满足不等式组的可行域如图所示:

(1)易求点A、B的坐标为:A(3,6),B(3,-6),
所以三角形OAB的面积为:
S△OAB=![]() ×12×3=18.
×12×3=18.
(2)目标函数化为:y=![]() x-
x-![]() ,画直线y=
,画直线y=![]() x及其平行线,当此直线经过A时,-
x及其平行线,当此直线经过A时,-![]() 的值最大,z的值最小,易求A 点坐标为(3,6),所以,z的最小值为3-2×6=-9.
的值最大,z的值最小,易求A 点坐标为(3,6),所以,z的最小值为3-2×6=-9.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】李强家这几年旅游消费情况如下表.
年份 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
金额/元 | 1000 | 1200 | 1500 | 1800 | 2000 | 2500 | 3000 | 3500 |
(1)根据上表数据绘制折线统计图.
李强家旅游消费情况统计图

(2)李强家平均每年旅游消费多少元?
(3)观察统计图,你发现了什么?