题目内容
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm.求△DEB的周长.
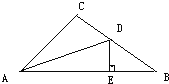
【答案】6厘米
【解析】
试题分析:由题目的已知条件应用AAS易证△CAD≌△EAD.得到DE=CD,于是BD+DE=BC=AC=AE,则周长可利用对应边相等代换求解.
解:因为AD平分∠CAB,∠C=90°,DE⊥AB,
所以∠CAD=∠BAD,∠C=∠AED.
又因为AD=AD,
在△CAD和△EAD中:
∠C=∠DEA,
∠CAD=∠DEA,
AD=AD,
所以△CAD≌△EAD,
所以AC=AE,CD=DE.
因为AC=BC,
所以BC=AE.
所以△DEB的周长为DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=6厘米.
答:△DEB的周长6厘米.

练习册系列答案
相关题目