题目内容
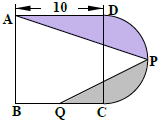 如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边BC 的中点,那么阴影部分面积是多少?(π=3.14)
如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边BC 的中点,那么阴影部分面积是多少?(π=3.14)分析:(1)连接PB,则阴影部分的面积等于图中正方形与半圆的面积之和减去空白部分两个三角形的面积;
(2)P点为半圆周的中点,作出三角形PAB的高PG,则G是AB的中点,所以PG的长度为10+10÷2=15厘米,所以它的面积是10×15÷2=75平方厘米;Q点为正方形一边的中点,所以三角形PBQ的面积是5×5÷2=12.5平方厘米;

(2)P点为半圆周的中点,作出三角形PAB的高PG,则G是AB的中点,所以PG的长度为10+10÷2=15厘米,所以它的面积是10×15÷2=75平方厘米;Q点为正方形一边的中点,所以三角形PBQ的面积是5×5÷2=12.5平方厘米;

解答:解:正方形和半圆的面积之和:10×10+3.14×(
)2÷2,
=100+39.25,
=139.25(平方厘米),
三角形PAB的面积是:10×15÷=75(平方厘米),
三角形PBQ的面积是5×5÷2=12.5(平方厘米),
则阴影部分的面积是:139.25-75-12.5=51.75(平方厘米);
答:阴影部分的面积是51.75平方厘米.
| 10 |
| 2 |
=100+39.25,
=139.25(平方厘米),
三角形PAB的面积是:10×15÷=75(平方厘米),
三角形PBQ的面积是5×5÷2=12.5(平方厘米),
则阴影部分的面积是:139.25-75-12.5=51.75(平方厘米);
答:阴影部分的面积是51.75平方厘米.
点评:此题考查了三角形、正方形和圆的面积公式的综合应用;连接BP,找出这两个白色三角形的高,求出空白部分的面积是解决本题的关键.

练习册系列答案
相关题目
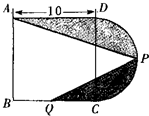 (2011?广州模拟)如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边的中点,求阴影部分面积.(单位:厘米)
(2011?广州模拟)如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边的中点,求阴影部分面积.(单位:厘米) 如图是由正方形和半圆组成的图形,其中P点为半圆周的中点,点Q为正方形一边的中点.求阴影部分的面积.
如图是由正方形和半圆组成的图形,其中P点为半圆周的中点,点Q为正方形一边的中点.求阴影部分的面积.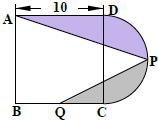 如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边BC 的中点,那么阴影部分面积是多少?(π=3.14)
如图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边BC 的中点,那么阴影部分面积是多少?(π=3.14)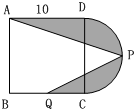 如图是由正方形和半圆组成的图形,其中P点为半圆周的中点,点Q为正方形一边的中点.求阴影部分的面积.
如图是由正方形和半圆组成的图形,其中P点为半圆周的中点,点Q为正方形一边的中点.求阴影部分的面积.