题目内容
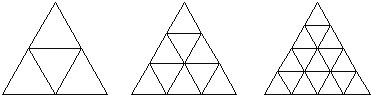
【题目】如图,将一个正三角形的每边分别2、3、4等分,得到的相同的小正三角形的个数依次是 、 、 ,如果将正三角形的每边10等分,那么,得到的相同的小正三角形有 个;如果正三角形被分成1225个相同的小正三角形,那么正三角形的每边被 等分.
【答案】4;9;16;100;35.
【解析】根据前边的特殊值,即图1中三角形的三条中位线把这个三角形分成了4个小的三角形,4=22;图2将分点连起来,可以看到整个三角形被分成了9个全等的三角形,9=32;把三条边都分成四等分,则将分点连起来,可以看到整个三角形被分成了16个全等的三角形,16=42,推而广之即可.
解:如果把三角形的每一条边二等分,将各个分点连起来,则三角形的三条中位线把这个三角形分成了4个小的三角形,4=22;
如果把三角形的每一条边三等分,将分点连起来,可以看到整个三角形被分成了9个全等的三角形,9=32;
把三条边都分成四等分,则将分点连起来,可以看到整个三角形被分成了16个全等的三角形,16=42;
如果把三条边都n等分,那么可以得到n2个这种小的全等三角形.
故当n=10时,102=100
当n2=1225时,因为35×35=1225,所以n=35.
故答案为:4;9;16;100;35.

练习册系列答案
相关题目
【题目】某校四年级同学喜欢健身运动情况统计表。
项目人数性别 | 羽毛球 | 跳绳 | 踢毽子 | 篮球 |
男生 | 30 | 25 | 10 | 80 |
女生 | 30 | 52 | 23 | 5 |
请根据以上数据制成复式条形统计图.
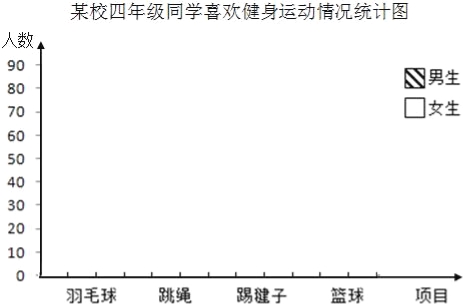
(1)喜欢什么项目的女生最多?喜欢什么项目的男生最少?
(2)喜欢什么项目的人最多?喜欢什么项目的人最少?
(3)你还能提出其他数学问题并解答吗?