题目内容
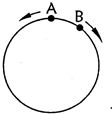 如图5,在长为490米的环形跑道上,A、B两点之间的跑道长50米,甲、乙两人同时从A、B两点出发反向奔跑.两人相遇后,乙立刻转身与甲同向奔跑,同时甲把速度提高了25%,乙把速度提高了20%.结果当甲跑到点A时,乙恰好跑到了点B.如果以后甲、乙的速度和方向都不变,那么当甲追上乙时,从一开始算起,甲一共跑了多少米?
如图5,在长为490米的环形跑道上,A、B两点之间的跑道长50米,甲、乙两人同时从A、B两点出发反向奔跑.两人相遇后,乙立刻转身与甲同向奔跑,同时甲把速度提高了25%,乙把速度提高了20%.结果当甲跑到点A时,乙恰好跑到了点B.如果以后甲、乙的速度和方向都不变,那么当甲追上乙时,从一开始算起,甲一共跑了多少米?分析:相遇后乙的速度提高20%,跑回B点,即来回路程相同,乙速度变化前后的比为5:6,所以所花时间的比为6:5.
设甲在相遇时跑了6个单位时间,则相遇后到跑回A点用了5个单位时间.
设甲原来每单位时间的速度V甲,由题意得:6V甲+5×V甲×(1+25%)=490,得:V甲=40(米).从A点到相遇点路程为40×6=240,所以V乙=(490-50-240)÷6=
(米).然后再求出两人速度变化后各自的速度;从相遇点开始,甲追上乙时,甲比乙多行一圈,进而求出甲一共跑的路程,解决问题.
设甲在相遇时跑了6个单位时间,则相遇后到跑回A点用了5个单位时间.
设甲原来每单位时间的速度V甲,由题意得:6V甲+5×V甲×(1+25%)=490,得:V甲=40(米).从A点到相遇点路程为40×6=240,所以V乙=(490-50-240)÷6=
| 100 |
| 3 |
解答:解:乙速度变化前后的比为1:(1+20%)=5:6,
所以所花时间的比为6:5.
设甲原来每单位时间的速度V甲,由题意得:
6V甲+5×V甲×(1+25%)=490,
6V甲+5×V甲×1.25=490,
得:V甲=40(米).
从A点到相遇点路程为:
40×6=240(米),
所以V乙为:
(490-50-240)÷6,
=200÷6,
=
(米).
两人速度变化后,甲的速度为:
40×(1+25%)=50(米),
乙的速度为:
×(1+20%),
=
×1.2,
=40(米),
从相遇点开始,甲追上乙时,甲比乙多行一圈,所以甲一共跑了:
490÷(50-40)×50+240,
=490÷10×50+240,
=49×50+240,
=2450+240,
=2690(米);
答:甲一共跑了2690米.
所以所花时间的比为6:5.
设甲原来每单位时间的速度V甲,由题意得:
6V甲+5×V甲×(1+25%)=490,
6V甲+5×V甲×1.25=490,
得:V甲=40(米).
从A点到相遇点路程为:
40×6=240(米),
所以V乙为:
(490-50-240)÷6,
=200÷6,
=
| 100 |
| 3 |
两人速度变化后,甲的速度为:
40×(1+25%)=50(米),
乙的速度为:
| 100 |
| 3 |
=
| 100 |
| 3 |
=40(米),
从相遇点开始,甲追上乙时,甲比乙多行一圈,所以甲一共跑了:
490÷(50-40)×50+240,
=490÷10×50+240,
=49×50+240,
=2450+240,
=2690(米);
答:甲一共跑了2690米.
点评:此题属于环形跑道问题,有一定难度,所以应认真分析,求出甲乙二人速度变化前后的速度是解答此题是的关键.

练习册系列答案
相关题目