题目内容
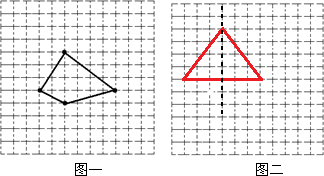
(2009?楚州区)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图(一)中四边形ABCD就是一个“格点四边形”.

(1)求图(一)中四边形ABCD的面积.
(2)在图(二)方格纸中画出一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.

(1)求图(一)中四边形ABCD的面积.
(2)在图(二)方格纸中画出一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.
分析:(1)根据毕克定理可得:格点面积=内部格点数+周界格点数÷2-1,观察图形可知,内部格点数是11,周界格点数是4,所以格点面积是11+4÷2-1=12;据此即可解答;
(2)三角形中,等腰三角形是轴对称图形,因为三角形的面积是12,所以这个等腰三角形的底可以是6,高是4,据此即可画图.
(2)三角形中,等腰三角形是轴对称图形,因为三角形的面积是12,所以这个等腰三角形的底可以是6,高是4,据此即可画图.
解答:解:(1)图(一)中四边形ABCD的面积是:
11+4÷2-1,
=11+2-1,
=12,
答:四边形ABCD的面积是12.
(2)等腰三角形是轴对称图形,因为三角形的面积是12,所以这个等腰三角形的底可以是6,高是4,画图如下:
11+4÷2-1,
=11+2-1,
=12,
答:四边形ABCD的面积是12.
(2)等腰三角形是轴对称图形,因为三角形的面积是12,所以这个等腰三角形的底可以是6,高是4,画图如下:

点评:此题主要考查利用毕克定理计算格点面积的方法以及画指定面积的三角形的方法,关键是明确等腰三角形是轴对称图形.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目