题目内容
填空.
(1)有民兵在操场上列队,只知人数在90-110之间,排成3列刚好无余,排成5列不足2人,排成7列不足4人,共有民兵________人.
(2)有一项工程,甲乙合作4天完成,乙丙合作5天完成,现甲丙合作2天后,剩下的乙独做5.5天完成.这项工程由乙做________天完成.
(3)一个分数,它的分子与分母之和是30,分子与分母各减去3后,这个分数的值是 ,原来的分数是________.
,原来的分数是________.
(4)将一个三角形的底边与高的长度都增加10%,那么新的三角形面积比原来的三角形面积增加了________%.
解:(1)3、5和7的最小公倍数是105,
105+3=108(人),
答:共有民兵108人;
(2)1÷(1- ×2-
×2- ×2)
×2)
=1÷(1- -
- )
)
=10(天),
答:这项工程由乙做10天完成;
(3)(30-3×2)÷(5+7)
=24÷12
=2,
原来的分子是2×5+3=13,分母是2×7+3=17
答:原来的分数是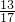 ;
;
(4)设原来的三角形的底为a,高为h,那么:
原来三角形的面积是: ah;
ah;
新三角形的底是:a×(1+10%)=1.1a,
新三角形的高是:h×(1+10%)=1.1h,
新三角形的面积是: ×1.1a×1.1h=
×1.1a×1.1h= ×(1.21ah),
×(1.21ah),
[ ×(1.21ah)-
×(1.21ah)- ah]÷
ah]÷ ah=1.21-1=0.21=21%,
ah=1.21-1=0.21=21%,
答:新的三角形面积比原来的三角形面积增加了21%.
故答案为:108;10;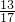 ;21%.
;21%.
分析:(1)由题意可知:排成3列无剩余,说明是3的倍数;排成5列不足2人,说明是5的倍数多3,排成7列不足4人,说明是7的倍数多3,要求共有民兵多少人求出3、5和7的最小公倍数加+3即可.
(2)甲丙合作2天后,剩下的乙单独作5天完成,等于是甲做2天,丙做2天,乙做5天即相当于甲乙合作2天,乙丙再合作2天,最后乙做1天完成;甲乙1天作 ,所以合作2天做
,所以合作2天做 ×2=
×2= ,乙丙1天作
,乙丙1天作 ,所以合作2天做
,所以合作2天做 ×2=
×2= ,还剩1-
,还剩1- -
- ,这些乙做1天完成,由此解答;
,这些乙做1天完成,由此解答;
(3)根据它的分子与分母的和是30,分子和分母各减去3之后得:分子与分母的和是30-2×3=24,所对应的份数是5+7=12份,1份就是24÷12=2,然后求出新的分子和分母各是多少进而求出原分数;
(4)设原来的三角形的底为a,高为h,求出这个三角形的面积;然后再把原来的底和高看成单位“1”,新的底和高是原来的1+10%,再求出新的面积,用新的面积减去原来的面积求出面积差,再用面积差除以原来的三角形的面积即可.
点评:这是一道综合性的应用题,解答时要认真审题,弄清要求问题与已知条件之间的关系细心解答.
105+3=108(人),
答:共有民兵108人;
(2)1÷(1-
 ×2-
×2- ×2)
×2)=1÷(1-
 -
- )
)=10(天),
答:这项工程由乙做10天完成;
(3)(30-3×2)÷(5+7)
=24÷12
=2,
原来的分子是2×5+3=13,分母是2×7+3=17
答:原来的分数是
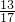 ;
;(4)设原来的三角形的底为a,高为h,那么:
原来三角形的面积是:
 ah;
ah;新三角形的底是:a×(1+10%)=1.1a,
新三角形的高是:h×(1+10%)=1.1h,
新三角形的面积是:
 ×1.1a×1.1h=
×1.1a×1.1h= ×(1.21ah),
×(1.21ah),[
 ×(1.21ah)-
×(1.21ah)- ah]÷
ah]÷ ah=1.21-1=0.21=21%,
ah=1.21-1=0.21=21%,答:新的三角形面积比原来的三角形面积增加了21%.
故答案为:108;10;
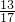 ;21%.
;21%.分析:(1)由题意可知:排成3列无剩余,说明是3的倍数;排成5列不足2人,说明是5的倍数多3,排成7列不足4人,说明是7的倍数多3,要求共有民兵多少人求出3、5和7的最小公倍数加+3即可.
(2)甲丙合作2天后,剩下的乙单独作5天完成,等于是甲做2天,丙做2天,乙做5天即相当于甲乙合作2天,乙丙再合作2天,最后乙做1天完成;甲乙1天作
 ,所以合作2天做
,所以合作2天做 ×2=
×2= ,乙丙1天作
,乙丙1天作 ,所以合作2天做
,所以合作2天做 ×2=
×2= ,还剩1-
,还剩1- -
- ,这些乙做1天完成,由此解答;
,这些乙做1天完成,由此解答;(3)根据它的分子与分母的和是30,分子和分母各减去3之后得:分子与分母的和是30-2×3=24,所对应的份数是5+7=12份,1份就是24÷12=2,然后求出新的分子和分母各是多少进而求出原分数;
(4)设原来的三角形的底为a,高为h,求出这个三角形的面积;然后再把原来的底和高看成单位“1”,新的底和高是原来的1+10%,再求出新的面积,用新的面积减去原来的面积求出面积差,再用面积差除以原来的三角形的面积即可.
点评:这是一道综合性的应用题,解答时要认真审题,弄清要求问题与已知条件之间的关系细心解答.

练习册系列答案
相关题目