题目内容
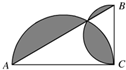已知三角形ABC是直角三角形，AC=4厘米，BC=2厘米，求阴影部分的面积．分析：如图：阴影部分的面积分别为甲、乙、丙，则空白部分的面积等于直径是4厘米的半圆的面积与直径是2厘米的半圆的面积减去甲、丙，2个乙的面积，而空白部分的面积还等于三角形ABC的面积减去乙的面积，由此即可求出阴影部分的面积．
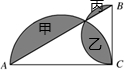
解答：解：3.14×（4÷2）2÷2+3.14×（2÷2）2÷2-甲-乙-丙-乙=4×2÷2-乙，
3.14×2+3.14÷2-甲-乙-丙=4，
甲+乙+丙=3.14×2+3.14÷2-4，
=6.28+1.57-4
=7.85-4，
=3.85（平方厘米）．
答：阴影部分的面积为3.85平方厘米．
3.14×2+3.14÷2-甲-乙-丙=4，
甲+乙+丙=3.14×2+3.14÷2-4，
=6.28+1.57-4
=7.85-4，
=3.85（平方厘米）．
答：阴影部分的面积为3.85平方厘米．
点评：关键是根据空白部分的面积与阴影部分的面积与半圆及三角形的关系，整体求出阴影部分的面积．
练习册系列答案
相关题目
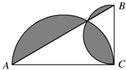已知三角形ABC是直角三角形，AC=4厘米，BC=2厘米，求阴影部分的面积．