题目内容
 图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=________平方厘米.
图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=________平方厘米.
75
分析:由图意可知:S△ABC=S△ADE+S正方形BDEF+S△EFC,设正方形的边长为a,再据题目所给数据,代入此等式,即可求出a的值,进而求出三角形ABC的面积.
解答:设正方形的边长为a,
则S△ABC=S△ADE+S正方形BDEF+S△EFC,
即 ×(9+a)×(4+a)=
×(9+a)×(4+a)= ×4×a+a2+
×4×a+a2+ ×9a,
×9a,
 a2+
a2+ a+2a+18=2a+
a+2a+18=2a+ a+a2,
a+a2,
 a2+18=a2,
a2+18=a2,
 a2=18,
a2=18,
a2=36;
所以a=6(厘米);
所以三角形ABC的面积为: ×(9+6)×(4+6),
×(9+6)×(4+6),
= ×15×10,
×15×10,
=75(平方厘米);
答:三角形ABC的面积是75平方厘米.
故答案为:75.
点评:解答此题的关键是:找出等量关系S△ABC=S△AFB+S正方形FBDE+S△EDC,即可列方程求解.
分析:由图意可知:S△ABC=S△ADE+S正方形BDEF+S△EFC,设正方形的边长为a,再据题目所给数据,代入此等式,即可求出a的值,进而求出三角形ABC的面积.
解答:设正方形的边长为a,
则S△ABC=S△ADE+S正方形BDEF+S△EFC,
即
 ×(9+a)×(4+a)=
×(9+a)×(4+a)= ×4×a+a2+
×4×a+a2+ ×9a,
×9a, a2+
a2+ a+2a+18=2a+
a+2a+18=2a+ a+a2,
a+a2, a2+18=a2,
a2+18=a2, a2=18,
a2=18,a2=36;
所以a=6(厘米);
所以三角形ABC的面积为:
 ×(9+6)×(4+6),
×(9+6)×(4+6),=
 ×15×10,
×15×10,=75(平方厘米);
答:三角形ABC的面积是75平方厘米.
故答案为:75.
点评:解答此题的关键是:找出等量关系S△ABC=S△AFB+S正方形FBDE+S△EDC,即可列方程求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 图中两块阴影部分的面积相等,三角形ABC是直角三角形,BC是直径,长20厘米.计算AB的长度.
图中两块阴影部分的面积相等,三角形ABC是直角三角形,BC是直径,长20厘米.计算AB的长度.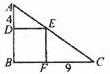 图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=
图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积= 如图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,三角形ABC是直角三角形,求BC的长.
如图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,三角形ABC是直角三角形,求BC的长.