题目内容
7.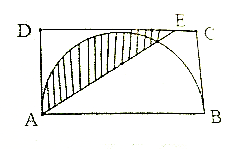 如图,长方形ABCD的宽AD=4厘米,DE=3EC,求阴影部分的面积.
如图,长方形ABCD的宽AD=4厘米,DE=3EC,求阴影部分的面积.
分析 因为长AD=4cm,DE=3EC,所以圆的半径是4÷2=2(厘米),四边形ADFO和四边形CBOF都是正方形,那么阴影部分的面积=正方形ADFO的面积+$\frac{1}{4}$圆的面积-三角形ADE的面积,据此解答即可.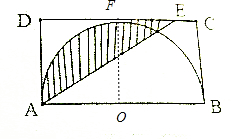
解答 解:圆的半径是4÷2=2(厘米),
阴影部分的面积:
2×2+$\frac{1}{4}$×3.14×22-4×4×2×$\frac{3}{4}$÷2
=4+12.56-12
=4.56(平方厘米)
答:阴影部分的面积是4.56平方厘米.
点评 本题考查了圆与组合图形的面积计算,这种类型的题可以根据几何图形的特征,通过分割、割补、平移、翻折、对称、旋转等方法,化复杂为简单,变组合图形为基本图形的加减组合.

练习册系列答案
相关题目