Question

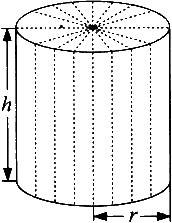
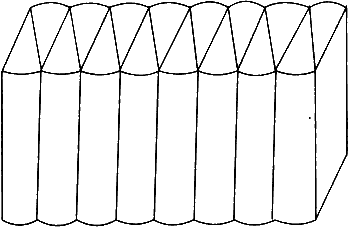
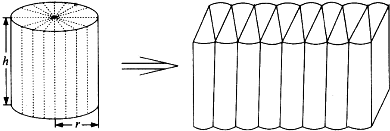
数学小组将一圆柱按左图切割开，然后拼为右图，观察填空．
拼出的右图是一个近似的

长方

体，它的高与圆柱的高

相等

，是

h

；它的底面积与圆柱的底面积

相等

，是

πr²

；拼出图形的体积是

πr²h

，圆柱的体积与它

相等

，所以圆柱的体积是

πr²h

．

Answer 1

分析：圆柱按左图切割开，然后拼为右图，拼成一个近似的长方体，它的高与圆柱的高相等，长方体的长等于=圆周长÷2=πγ，宽=圆的半径=γ，所以长方体的体积是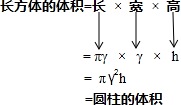：（见图）
由于体积不变，所以圆柱的体积就等于长方体的体积，即圆柱的体积：V=πr²h．

解答：解：拼出的右图是一个近似的长方体，它的高与圆柱的高相等，是h；
它的底面积与圆柱的底面积相等，是πr²；
拼出图形的体积是πr²h，圆柱的体积与它相等，
所以圆柱的体积是πr²h．
故答案为：长方，相等，h，相等，πr² 相等，πr²h．

点评：此题主要是利用等积变形，将圆柱进行割补，变成比较容易求体积的长方体．本题实际考查了圆柱体积的公式推导，需要结合操作理解记忆，不要死记硬背．