题目内容
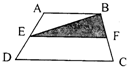 如图ABCD是一个任意的梯形,它的面积是68平方厘米,E、F分别是AD与BC的中点,阴影部分的面积是________平方厘米.
如图ABCD是一个任意的梯形,它的面积是68平方厘米,E、F分别是AD与BC的中点,阴影部分的面积是________平方厘米.
17
分析:如下图:连接DF,设梯形的高为h,根据E、F分别是AD与BC的中点,知道三角形ABE、三角形BEF、三角形DEF、三角形DCF的高是 h,由此根据三角形ABE、三角形BEF、三角形DEF、三角形DCF的面积和就是梯形的面积,即可求出阴影部分的面积.
h,由此根据三角形ABE、三角形BEF、三角形DEF、三角形DCF的面积和就是梯形的面积,即可求出阴影部分的面积.

解答:S△ABE= ×
× AB×h,
AB×h,
S△BEF= ×
× ×EF×h,
×EF×h,
S△DEF= ×
× ×EF×h,
×EF×h,
S△DFC= ×
× ×CD×h,
×CD×h,
所以:S△ABE+S△BEF+S△DEF+S△DFC= ×
× AB×h+
AB×h+ ×
× ×EF×h+
×EF×h+ ×
× ×EF×h+
×EF×h+ ×
× ×CD×h=68,
×CD×h=68,
而AB+CD=2EF,
所以,4EF×h=68×4,
EF×h=68;
所以阴影部分的面积为:S△BEF= ×
× ×EF×h,
×EF×h,
= ×68,
×68,
=17(平方厘米);
故答案为:17.
点评:解答此题的关键是根据三角形与梯形的关系,求出EF与梯形的高的乘积,然后整体代入即可求出阴影部分的面积.
分析:如下图:连接DF,设梯形的高为h,根据E、F分别是AD与BC的中点,知道三角形ABE、三角形BEF、三角形DEF、三角形DCF的高是
 h,由此根据三角形ABE、三角形BEF、三角形DEF、三角形DCF的面积和就是梯形的面积,即可求出阴影部分的面积.
h,由此根据三角形ABE、三角形BEF、三角形DEF、三角形DCF的面积和就是梯形的面积,即可求出阴影部分的面积.
解答:S△ABE=
 ×
× AB×h,
AB×h,S△BEF=
 ×
× ×EF×h,
×EF×h,S△DEF=
 ×
× ×EF×h,
×EF×h,S△DFC=
 ×
× ×CD×h,
×CD×h,所以:S△ABE+S△BEF+S△DEF+S△DFC=
 ×
× AB×h+
AB×h+ ×
× ×EF×h+
×EF×h+ ×
× ×EF×h+
×EF×h+ ×
× ×CD×h=68,
×CD×h=68,而AB+CD=2EF,
所以,4EF×h=68×4,
EF×h=68;
所以阴影部分的面积为:S△BEF=
 ×
× ×EF×h,
×EF×h,=
 ×68,
×68,=17(平方厘米);
故答案为:17.
点评:解答此题的关键是根据三角形与梯形的关系,求出EF与梯形的高的乘积,然后整体代入即可求出阴影部分的面积.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
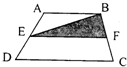 如图ABCD是一个任意的梯形,它的面积是68平方厘米,E、F分别是AD与BC的中点,阴影部分的面积是
如图ABCD是一个任意的梯形,它的面积是68平方厘米,E、F分别是AD与BC的中点,阴影部分的面积是