题目内容
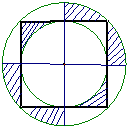 图中,正方形ABCD的边长为10厘米,过它的四个顶点作液体个大圆,过它的各边中点作一个小圆,再过两组对边中点作直线,求图中各块阴影部分的面积总和.(?π=3.14)
图中,正方形ABCD的边长为10厘米,过它的四个顶点作液体个大圆,过它的各边中点作一个小圆,再过两组对边中点作直线,求图中各块阴影部分的面积总和.(?π=3.14)分析:如图所示,将阴影①、②、③分别移到空白①、②、③的位置,则可以得出阴影部分的面积就等于环形面积的一半,利用圆环的面的计算方法即可得解.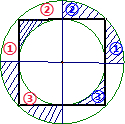

解答:解:据分析可知:大圆的面积为:
π×直径2,
其中大圆的直径2=102+102=200,
所以大圆的面积为:
π×直径2=50π,
小圆的面积为:
π×直径2=
π(
)2=
π,
所以图中阴影部分的总面积等于:
(50-
)π=
π=29.4375(平方厘米);
答:图中各块阴影部分的面积总和为29.4375平方厘米.
| 1 |
| 4 |
其中大圆的直径2=102+102=200,
所以大圆的面积为:
| 1 |
| 4 |
小圆的面积为:
| 1 |
| 4 |
| 1 |
| 4 |
| 10 |
| 2 |
| 25 |
| 4 |
所以图中阴影部分的总面积等于:
| 1 |
| 2 |
| 25 |
| 4 |
| 75 |
| 8 |
答:图中各块阴影部分的面积总和为29.4375平方厘米.
点评:利用平移的方法,得出阴影部分的面积即为大圆与小圆之间的圆环面积的一半,是解答本题的关键.

练习册系列答案
相关题目
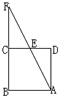 在图中,正方形ABCD的面积比三角形ABF的面积小6平方厘米,线段AB长8厘米,CF长是
在图中,正方形ABCD的面积比三角形ABF的面积小6平方厘米,线段AB长8厘米,CF长是 在如图中,正方形ABCD的边长是4厘米,E、F分别是边AB和BC的中点,求四边形BFGE的面积.
在如图中,正方形ABCD的边长是4厘米,E、F分别是边AB和BC的中点,求四边形BFGE的面积.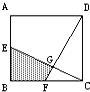 在图中,正方形ABCD的边长是5,E,F分别是AB和BC的中点,求:四边形BFGE的面积是
在图中,正方形ABCD的边长是5,E,F分别是AB和BC的中点,求:四边形BFGE的面积是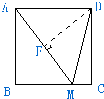 (2009?湛江模拟)如图中,正方形ABCD的边长是8厘米,AM长是10厘米.求DF的长.
(2009?湛江模拟)如图中,正方形ABCD的边长是8厘米,AM长是10厘米.求DF的长.