题目内容
20.把一条纸带平均分成8份,4份涂红色,3份涂蓝色,其余的不涂色.
(1)红色和蓝色部分一共占这条纸带的$\frac{()}{()}$.
(2)涂色部分比剩余部分多占这条纸带的$\frac{()}{()}$.
分析 (1)把这条纸带的长度看作单位“1”,把它平均分成8份,每份是它的$\frac{1}{8}$,其中4份涂红色,也就是涂红色的是4个$\frac{1}{8}$,即$\frac{4}{8}$,3份涂蓝色,也就是涂蓝色的是3个$\frac{1}{8}$,即$\frac{3}{8}$,这样涂色红色和蓝色的是(4+3)个$\frac{1}{8}$,即$\frac{7}{8}$;剩余部分是1份,即剩余部分是$\frac{1}{8}$.
(2)用涂色部分所占的分率减去剩余部分所占的分率,就是涂色部分比剩余部分多占这条纸带的分率.或求出涂色部分比剩余部分多几份,就是涂色部分比剩余部分多占这条纸带的八份之几.
解答 解:(1)如图:
红色和蓝色部分一共占这条纸带的$\frac{7}{8}$;
(2)$\frac{7}{8}$-$\frac{1}{8}$=$\frac{6}{8}$
即涂色部分比剩余部分多占这条纸带的$\frac{6}{8}$.
故答案为:$\frac{7}{8}$,$\frac{6}{8}$.
点评 本题是考查分数的意义.把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.青岛在日照的东北方向,日照在青岛的( )方向.
| A. | 东南 | B. | 西南 | C. | 西北 |
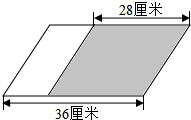 如图,一个平行四边形,它的底减少了28厘米,面积就减少了420平方厘米(阴影部分),原来这个平行四边形的面积是多少?
如图,一个平行四边形,它的底减少了28厘米,面积就减少了420平方厘米(阴影部分),原来这个平行四边形的面积是多少?
 ,
,
 .
.