题目内容
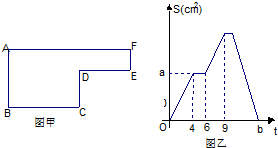 已知动点P以每秒2cm的速度沿图甲的边框按 B→C→D→E→F→A 的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,则图甲中的图形面积是
已知动点P以每秒2cm的速度沿图甲的边框按 B→C→D→E→F→A 的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,则图甲中的图形面积是60平方厘米
60平方厘米
,图乙中的a与b的值分别是24平方厘米,17秒,
24平方厘米,17秒,
.分析:根据图例知:图中P点的运动与相应的△ABP的面积S与时间t之间的关系用图乙来表示,从图中可知,当P运动4秒是到达C点中,这是BC的长度就是2×4厘米,P从C点运动到D点用了6-4秒,CD的长度就是(6-4)×2厘米,P点从D运动到E用了9-6秒,DE和长度就是(9-6)×2厘米,EF和长度就是AB-CD,AF的长度就是BC+DE.据此解答.
解答:解:根据以上分析知:
BC的长度是:
2×4=8(厘米),
CD的长度是:
(6-4)×2,
=2×2,
=4(厘米),
DE的长度是:
(9-6)×2,
=3×2,
=6(厘米),
EF=AB-CD=6-4=2(厘米),
AF=BC+DE=8+6=14(厘米),
图甲的面积是:
6×8+6×2,
=48+12,
=60(平方厘米),
a的值是:
×AB×BC,
=
×6×8,
=24(平方厘米),
b的值是:
9+2÷2+14÷2,
=9+1+7,
=17(秒).
答:甲中的图形面积是60平方厘米,图乙中的a与b的值分别是24平方厘米,17秒.
故答案为:60平方厘米,24平方厘米,17秒.
BC的长度是:
2×4=8(厘米),
CD的长度是:
(6-4)×2,
=2×2,
=4(厘米),
DE的长度是:
(9-6)×2,
=3×2,
=6(厘米),
EF=AB-CD=6-4=2(厘米),
AF=BC+DE=8+6=14(厘米),
图甲的面积是:
6×8+6×2,
=48+12,
=60(平方厘米),
a的值是:
| 1 |
| 2 |
=
| 1 |
| 2 |
=24(平方厘米),
b的值是:
9+2÷2+14÷2,
=9+1+7,
=17(秒).
答:甲中的图形面积是60平方厘米,图乙中的a与b的值分别是24平方厘米,17秒.
故答案为:60平方厘米,24平方厘米,17秒.
点评:本题的关键是让学生看明白图乙中P点的移动规律.

练习册系列答案
相关题目
 如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求:
如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求: 在长方形ABCD中,AB=120厘米,点Q以每秒3厘米的速度从A向B运动,点P以每秒4厘米的速度从C向D运动,两点同时运动多少秒后,P,Q的连线将长方形ABCD的面积分成3:5两部分?
在长方形ABCD中,AB=120厘米,点Q以每秒3厘米的速度从A向B运动,点P以每秒4厘米的速度从C向D运动,两点同时运动多少秒后,P,Q的连线将长方形ABCD的面积分成3:5两部分? 如图,在等边三角形ABC上有两个动点D、E,动点D从A出发到B,每秒移动1厘米,动点E以每秒4厘米的速度在AC间往返运动.D、E两点同时从A点出发,随时连结DE两点,在D由A到B的这段时间内,线段DE与三角形的一部分构成的最小梯形面积是18平方厘米(图中阴影部分).三角形ABC的面积是多少平方厘米?
如图,在等边三角形ABC上有两个动点D、E,动点D从A出发到B,每秒移动1厘米,动点E以每秒4厘米的速度在AC间往返运动.D、E两点同时从A点出发,随时连结DE两点,在D由A到B的这段时间内,线段DE与三角形的一部分构成的最小梯形面积是18平方厘米(图中阴影部分).三角形ABC的面积是多少平方厘米? 已知动点P以每秒2cm的速度沿图甲的边框按 B→C→D→E→F→A 的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,则图甲中的图形面积是________,图乙中的a与b的值分别是________.
已知动点P以每秒2cm的速度沿图甲的边框按 B→C→D→E→F→A 的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,则图甲中的图形面积是________,图乙中的a与b的值分别是________.