题目内容
 图中有11条直线.请将1至11这11个数分别填在11个圆圈里,使每一条直线上所有数的和相等.求这个相等的和以及标有*的圆圈中所填的数.
图中有11条直线.请将1至11这11个数分别填在11个圆圈里,使每一条直线上所有数的和相等.求这个相等的和以及标有*的圆圈中所填的数.分析:如下图,在每个圆圈内标上字母,带有*的圆圈标为x,设每条直线上数字之和为S,找出所有的直线的和,利用每一条直线上所有数的和相等,列出等式,再根据字母出现次数的多少,
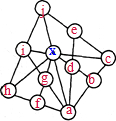

解答:解:如上图所示,在每个圆圈内标上字母,带有*的圆圈标为x,
首先考虑以下四条直线:(h、f、a),(i、g、a),(x、d、b),(j、e、c),除了标有a的圆圈外,其余每个圆圈都出现了一次,而标有a的圆圈出现了两次,
设每条直线上数字之和为S,
则有:(1+11)×11÷2+a=4S,即66+a=4S,
再考虑以下五条直线:(h、f、a),(i、g、a),(j、x、a),(e、d、a),(c、b、a),
同理我们可得到66+4a=5S;综合两个等式,可得a为6,每条直线上和S为18;
最后考虑含x的五条直线:(x、h),(x、g、f),(j、x、a),(x、d、b),(i、x、c).其中除了x出现了5次,e没有出现,其他数字均只出现了一次,
于是可以得到:66+4x-e=5S=90,即4x-e=24,由e是1-11间的数且e≠x可知x=7;
即每行相等的和S为18,*所填的数为7.
答:这个相等的和是18,标有*的圆圈中所填的数是7.
首先考虑以下四条直线:(h、f、a),(i、g、a),(x、d、b),(j、e、c),除了标有a的圆圈外,其余每个圆圈都出现了一次,而标有a的圆圈出现了两次,
设每条直线上数字之和为S,
则有:(1+11)×11÷2+a=4S,即66+a=4S,
再考虑以下五条直线:(h、f、a),(i、g、a),(j、x、a),(e、d、a),(c、b、a),
同理我们可得到66+4a=5S;综合两个等式,可得a为6,每条直线上和S为18;
最后考虑含x的五条直线:(x、h),(x、g、f),(j、x、a),(x、d、b),(i、x、c).其中除了x出现了5次,e没有出现,其他数字均只出现了一次,
于是可以得到:66+4x-e=5S=90,即4x-e=24,由e是1-11间的数且e≠x可知x=7;
即每行相等的和S为18,*所填的数为7.
答:这个相等的和是18,标有*的圆圈中所填的数是7.
点评:关键是在每个圆圈内标上字母,再根据每一条直线上所有数的和相等,列出等式解答.

练习册系列答案
相关题目
 如图所示,在一个面积为1920000平方米的长方形货场中有一条长为1600米的直线铁路AE.现有一辆装满货物的卡车停放在D点.如果卡车的速度是每分钟100米,请计算说明该卡车11分钟内能否将这车货物运到铁路线旁.
如图所示,在一个面积为1920000平方米的长方形货场中有一条长为1600米的直线铁路AE.现有一辆装满货物的卡车停放在D点.如果卡车的速度是每分钟100米,请计算说明该卡车11分钟内能否将这车货物运到铁路线旁.