题目内容
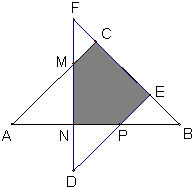 如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.
如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.
26
分析:由题意可知:阴影部分的面积=S△FNB-S△CFM-S△PBE,求S△FED的面积需要知道BF的长度,求S△CFM和S△PBE需要求出FC和BE的长度,由“BC=10,EF=8,CE=FC+BE”可知:2FC+BE=8①,2BE+FC=10②,由①和②即可求出FC和BE的值,从而问题逐步得解.
解答:由题意可知:2FC+BE=8①,
2BE+FC=10②,
由①得:BE=8-2FC③,
将③代入②得:
2×(8-2FC)+FC=10,
16-4FC+FC=10,
3FC=6,
FC=2;
BE=8-2×2=4;
所以BF=2×(2+4),
=2×6,
=12;
阴影部分的面积= ×12×(
×12×( ×12)-
×12)- ×2×2-
×2×2- ×4×4,
×4×4,
=6×6-2-8,
=36-10,
=26;
故答案:26.
点评:解答此题关键是先求出FC和BE的长度,进而利用阴影部分的面积=S△FNB-S△CFM-S△PBE,即可求解.
分析:由题意可知:阴影部分的面积=S△FNB-S△CFM-S△PBE,求S△FED的面积需要知道BF的长度,求S△CFM和S△PBE需要求出FC和BE的长度,由“BC=10,EF=8,CE=FC+BE”可知:2FC+BE=8①,2BE+FC=10②,由①和②即可求出FC和BE的值,从而问题逐步得解.
解答:由题意可知:2FC+BE=8①,
2BE+FC=10②,
由①得:BE=8-2FC③,
将③代入②得:
2×(8-2FC)+FC=10,
16-4FC+FC=10,
3FC=6,
FC=2;
BE=8-2×2=4;
所以BF=2×(2+4),
=2×6,
=12;
阴影部分的面积=
 ×12×(
×12×( ×12)-
×12)- ×2×2-
×2×2- ×4×4,
×4×4,=6×6-2-8,
=36-10,
=26;
故答案:26.
点评:解答此题关键是先求出FC和BE的长度,进而利用阴影部分的面积=S△FNB-S△CFM-S△PBE,即可求解.

练习册系列答案
相关题目


 =
=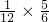 =
= =
=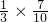 =
= =
=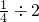 =
= 等于某数的16%,某数是________;甲数比乙数少20%,乙数就比甲数多________.
等于某数的16%,某数是________;甲数比乙数少20%,乙数就比甲数多________.