题目内容
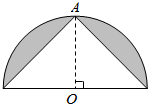
6. 如图,把这个圆柱体削成最大的圆锥体,圆锥体的体积是这个圆柱体体积的$\frac{1}{3}$,削去部分的体积是25.12dm3.
如图,把这个圆柱体削成最大的圆锥体,圆锥体的体积是这个圆柱体体积的$\frac{1}{3}$,削去部分的体积是25.12dm3.
分析 圆锥的体积=$\frac{1}{3}$×底面积×高,圆柱的体积=底面积×高;若圆锥与圆柱等底等高,则圆锥的体积是圆柱体积的$\frac{1}{3}$;由题意可知:这个最大的圆锥与圆柱等底等高,圆柱的体积已知,从而可以求出圆锥的体积,圆柱的体积减去圆锥的体积,就是削去部分的体积.
解答 解:等底等高的圆锥的体积是圆柱体积的$\frac{1}{3}$
削去部分的体积:
3.14×22×3×(1-$\frac{1}{3}$)
=3.14×4×2
=25.12(立方分米)
答:圆锥体的体积是这个圆柱体体积的$\frac{1}{3}$,削去部分的体积是25.12dm3.
故答案为:$\frac{1}{3}$,25.12.
点评 解答此题的主要依据是:圆锥的体积是与其等底等高的圆柱体积的$\frac{1}{3}$.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

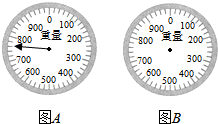 小明放了一些苹果在秤上,指针显示了这些苹果的重量(见图A).他拿走了一个苹果,指针下降了120克.现在苹果有640克,在图B上画出现在指针所在的位置.
小明放了一些苹果在秤上,指针显示了这些苹果的重量(见图A).他拿走了一个苹果,指针下降了120克.现在苹果有640克,在图B上画出现在指针所在的位置.