题目内容
一块长方体木材,长80厘米、宽20厘米、厚5厘米,若锯成最大的正方体木块(要求不能割补,不能浪费),可以锯成________块,每块体积应是________立方厘米.
64 125
分析:根据长方体切割正方体的方法可知:要使木块的体积最大,木料又不能有剩余,那么正方体木块的棱长应该是80、20和5的最大公因数,求出它们的最大公约数是5,然后根据锯出的总块数等于长宽高上锯成的块数的连乘积.由此即可解答.
解答:因为80、20和5的最大公约数是5,要使木块的体积最大,木料又不能有剩余,
所以正方体木块的棱长应该是5厘米,
(80÷5)×(20÷5)×(5÷5),
=16×4×1,
=64(块);
每一块的体积是:5×5×5=125(立方厘米),
答:可以锯成64块,每一块的体积是125立方厘米.
故答案为:64;125.
点评:解答此题的关键是:明确小正方体的棱长是原长方体的长宽高的长度的最大公约数以及锯出的总块数等于长宽高上锯成的块数的连乘积.
分析:根据长方体切割正方体的方法可知:要使木块的体积最大,木料又不能有剩余,那么正方体木块的棱长应该是80、20和5的最大公因数,求出它们的最大公约数是5,然后根据锯出的总块数等于长宽高上锯成的块数的连乘积.由此即可解答.
解答:因为80、20和5的最大公约数是5,要使木块的体积最大,木料又不能有剩余,
所以正方体木块的棱长应该是5厘米,
(80÷5)×(20÷5)×(5÷5),
=16×4×1,
=64(块);
每一块的体积是:5×5×5=125(立方厘米),
答:可以锯成64块,每一块的体积是125立方厘米.
故答案为:64;125.
点评:解答此题的关键是:明确小正方体的棱长是原长方体的长宽高的长度的最大公约数以及锯出的总块数等于长宽高上锯成的块数的连乘积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
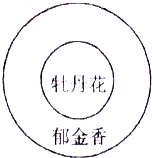 植物园的一处风景由两个同心圆构成,外圆直径50米,内圆直径30米,内圆栽种牡丹花,外面环形部分栽种郁金香,请用简便方法计算郁金香的占地面积.(π取3.14)
植物园的一处风景由两个同心圆构成,外圆直径50米,内圆直径30米,内圆栽种牡丹花,外面环形部分栽种郁金香,请用简便方法计算郁金香的占地面积.(π取3.14)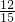 =20÷________=________%
=20÷________=________% ,小圆面积是大圆面积的________.
,小圆面积是大圆面积的________.