题目内容
求阴影部分的面积.
已知△ABC中,BC=48厘米,AD=21厘米,AD=3MD.

已知△ABC中,BC=48厘米,AD=21厘米,AD=3MD.

分析:因为三角形的面积=
×底×高,底一定时,三角形的面积与高成正比例,又因为AD=3MD,所以三角形ABC的面积等于三角形MBC的面积的3倍,则阴影部分的面积是三角形ABC的面积的
,据此利用三角形的面积公式求出三角形ABC的面积,再乘
,即可求出阴影部分的面积.
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:根据题干分析可得:因为AD=3MD
所以三角形ABC的面积等于三角形MBC的面积的3倍
则阴影部分的面积是三角形ABC的面积的
48×21÷2×
=336(平方厘米)
答:阴影部分的面积是336平方厘米.
所以三角形ABC的面积等于三角形MBC的面积的3倍
则阴影部分的面积是三角形ABC的面积的
| 2 |
| 3 |
48×21÷2×
| 2 |
| 3 |
答:阴影部分的面积是336平方厘米.
点评:此题考查三角形的底一定时,三角形的与高成正比例的性质的灵活应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 (2012?金沙县)如图,求阴影部分的面积.已知:r=10cm.
(2012?金沙县)如图,求阴影部分的面积.已知:r=10cm. 求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积90平方厘米.
求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积90平方厘米.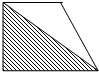 求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积90平方厘米.
求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积90平方厘米.