题目内容
16.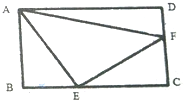 长方形ABCD的面积是40,△ABE的面积是8,△ADF的面积是10,求△AEF的面积.
长方形ABCD的面积是40,△ABE的面积是8,△ADF的面积是10,求△AEF的面积.
分析 三角形ABE的面积是长方形面积的:8÷40=$\frac{1}{5}$,所以BE是BC的$\frac{1}{5}$×2=$\frac{2}{5}$,即EC是BC的1-$\frac{2}{5}$=$\frac{3}{5}$;同理,三角形ADF的面积是长方形面积的:10÷40=$\frac{1}{4}$,则DF是DC的$\frac{1}{2}$,即FC是DC的1-$\frac{1}{2}$=$\frac{1}{2}$;所以三角形EFC是长方形面积的$\frac{3}{5}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{3}{20}$,其面积是:40×$\frac{3}{20}$=6平方厘米,然后用长方形ABCD的面积分别减去三个三角形的面积,就是三角形AEF的面积,据此解答即可.
解答 解:三角形ABE的面积是长方形面积的:8÷40=$\frac{1}{5}$,所以BE是BC的$\frac{1}{5}$×2=$\frac{2}{5}$,即EC是BC的1-$\frac{2}{5}$=$\frac{3}{5}$;
同理,三角形ADF的面积是长方形面积的:10÷40=$\frac{1}{4}$,则DF是DC的$\frac{1}{2}$,即FC是DC的1-$\frac{1}{2}$=$\frac{1}{2}$;
所以三角形EFC是长方形面积的$\frac{3}{5}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{3}{20}$,其面积是:40×$\frac{3}{20}$=6平方厘米,
所以,三角形AEF的面积是:
40-8-10-6=16(平方厘米)
答:△AEF的面积是16平方厘米.
点评 本题考查了比较复杂的三角形面积求法的灵活应用,关键是求出△CEF的直角边EC和CF各占长方形的长和宽的几分之几.

 阅读快车系列答案
阅读快车系列答案| 420÷60= | 120÷30= | 240÷80= | 80÷40= |
| 240÷30= | 630÷90= | 350÷70= | 480÷80= |
| 130-50= | 400÷50= | 720÷90= | 330÷30= |