题目内容
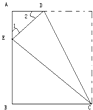 一张长方形纸折成如图梯形的形状,∠1=∠2=45度,AB边长10CM,求梯形ABCD的面积.
一张长方形纸折成如图梯形的形状,∠1=∠2=45度,AB边长10CM,求梯形ABCD的面积.分析:如图,因为∠1=∠2,所以AE=AD,又由于∠DEC是原长方形的一个角,是90°,∠B=90°,从而可以推出△AEC是等腰三角形,即BE=BC,由于梯形的面积=
(AD+BC)×AB,把AD用AE代换,把BC用BE代换,由于AE+BE=AB,梯形的面积=
AB×AB,又知AB=10cm,从而可以求出梯形的面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图
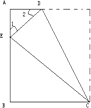
因为∠A是直角,∴∠1=∠2=45°,所以AE=AD,
又因为∠CDE=90°(原长方形的一个角),
所以∠BEC=∠=45°,所以BE=CE,
所以梯形ABCD的面积=
(AD+BC)×AB=
(AE+BE)×AB=
×10×10=50(平方厘米 );
故答案为:50平方厘米

因为∠A是直角,∴∠1=∠2=45°,所以AE=AD,
又因为∠CDE=90°(原长方形的一个角),
所以∠BEC=∠=45°,所以BE=CE,
所以梯形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:50平方厘米
点评:本题是考查简单图形的折叠问题、梯形的面积等.解答此题的关键是通过等量代换,梯形上底+下底=梯形的高.

练习册系列答案
相关题目
把一张长方形纸折成如图时,其中∠1和∠2相等,那么∠1=( )
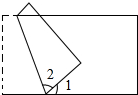

| A、90° | B、45° | C、60° |
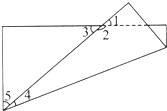 把一张长方形纸折成如图的形状,已知∠1+∠2+∠3=220°,∠4=20°,求∠1、∠2、∠3、∠5各是多少度.
把一张长方形纸折成如图的形状,已知∠1+∠2+∠3=220°,∠4=20°,求∠1、∠2、∠3、∠5各是多少度. (2012?丰润区)一张长方形纸折成如图样子,角1是58度,角2是
(2012?丰润区)一张长方形纸折成如图样子,角1是58度,角2是 一张长方形纸折成如图梯形的形状,∠1=∠2=45度,AB边长10CM,求梯形ABCD的面积.
一张长方形纸折成如图梯形的形状,∠1=∠2=45度,AB边长10CM,求梯形ABCD的面积.