题目内容
把一个体积是189立方厘米的圆柱形铁棒和一个棱长是5厘米的正方体铁块熔成一个半径是1厘米的圆锥形铁块,铸成的圆锥形铁块的高是多少?
解:189+5×5×5=314(立方厘米),
314×3÷(3.14×1×1),
=942÷3.14,
=300(厘米),
答:这个圆锥形铁块的高是300厘米.
分析:熔铸前后的体积不变,所以先利用正方体的体积公式求出这两块铁块的体积之和,再利用圆锥的体积公式可得:圆锥的高=体积×3÷底面积,据此计算即可解答.
点评:此题考查正方体、圆锥体的体积公式的计算应用,抓住熔铸前后的体积不变,是解决本题的关键.
314×3÷(3.14×1×1),
=942÷3.14,
=300(厘米),
答:这个圆锥形铁块的高是300厘米.
分析:熔铸前后的体积不变,所以先利用正方体的体积公式求出这两块铁块的体积之和,再利用圆锥的体积公式可得:圆锥的高=体积×3÷底面积,据此计算即可解答.
点评:此题考查正方体、圆锥体的体积公式的计算应用,抓住熔铸前后的体积不变,是解决本题的关键.

练习册系列答案
相关题目
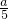 是假分数,同时使
是假分数,同时使 六分之a是真分数,a应该为
六分之a是真分数,a应该为 +
+ -
- )÷
)÷
 ÷
÷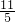 +
+ ×
×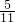 +
+ -
- χ=
χ=