题目内容
直角三角形的三边长是3、4、5厘米,以斜边所在直线为轴旋转,形成一立体图形,试求该立体图形的体积.
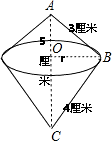
解:直角三角形斜边所在直线为轴旋转一周,得到的几何体是同一底面的两个圆锥,如上图所示,
设这个圆锥的底面半径是r,则:
5r÷2=3×4÷2,
5r=12,
r=2.4,
所以这个立体图形的体积是:
 ×3.14×2.42×(AO+CO),
×3.14×2.42×(AO+CO),
= ×3.14×5.76×5;
×3.14×5.76×5;
=30.114(立方厘米),
答:旋转一周后的立体图形的体积是30.114立方厘米.
分析:直角三角形斜边所在直线为轴旋转一周,得到的几何体是同一底面的两个圆锥,用直角三角形的面积求出底面圆的半径,然后用圆锥的体积公式求出几何体的体积.
点评:本题考查的是圆锥的计算,以直角三角形斜边所在的直线为轴转动一周,得到的几何体是两个圆锥,用圆锥的体积公式求出这个几何体的体积.
设这个圆锥的底面半径是r,则:
5r÷2=3×4÷2,
5r=12,
r=2.4,
所以这个立体图形的体积是:
 ×3.14×2.42×(AO+CO),
×3.14×2.42×(AO+CO),=
 ×3.14×5.76×5;
×3.14×5.76×5;=30.114(立方厘米),
答:旋转一周后的立体图形的体积是30.114立方厘米.
分析:直角三角形斜边所在直线为轴旋转一周,得到的几何体是同一底面的两个圆锥,用直角三角形的面积求出底面圆的半径,然后用圆锥的体积公式求出几何体的体积.

点评:本题考查的是圆锥的计算,以直角三角形斜边所在的直线为轴转动一周,得到的几何体是两个圆锥,用圆锥的体积公式求出这个几何体的体积.

练习册系列答案
相关题目