题目内容
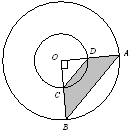 (2012?广东)如图,阴影部分的面积是25平方米,求圆环面积.(π取3.14)
(2012?广东)如图,阴影部分的面积是25平方米,求圆环面积.(π取3.14)分析:设大圆的半径为R,小圆的半径为r,则圆环的面积=大圆的面积-小圆的面积,阴影部分的面积=大三角形的面积-小三角形的面积,即R×R×
-r×r×
=
-
,于是可以用两圆的半径表示出阴影部分的面积,进而可以求出圆环的面积.
| 1 |
| 2 |
| 1 |
| 2 |
| R2 |
| 2 |
| r2 |
| 2 |
解答:解:设大圆的半径为R,小圆的半径为r,
阴影部分的面积:
-
=25,
于是可得R2-r2=50(平方米),
所以圆环的面积:π×(R2-r2),
=3.14×50,
=157(平方米);
答:圆环的面积是157平方米.
阴影部分的面积:
| R2 |
| 2 |
| r2 |
| 2 |
于是可得R2-r2=50(平方米),
所以圆环的面积:π×(R2-r2),
=3.14×50,
=157(平方米);
答:圆环的面积是157平方米.
点评:解答此题的关键是:设出半径,利用阴影部分的面积求得圆环的面积.

练习册系列答案
相关题目
 (2012?广东)如图是牛肉的成分统计图.如果这块牛肉重500克,脂肪占这块牛肉的
(2012?广东)如图是牛肉的成分统计图.如果这块牛肉重500克,脂肪占这块牛肉的 等底等高的圆柱与圆锥摆放如图,它们从左面看到的是( )
等底等高的圆柱与圆锥摆放如图,它们从左面看到的是( ) (2012?广东)学校的跳远沙池长6.28米,宽2米,学校运来一堆沙子(堆放如图).如果把这些沙子均匀地铺在跳远沙池中,可以铺多厚?
(2012?广东)学校的跳远沙池长6.28米,宽2米,学校运来一堆沙子(堆放如图).如果把这些沙子均匀地铺在跳远沙池中,可以铺多厚?