题目内容
【题目】已知,点O为直线AB上一点,∠COD=90°,0E是∠AOD的平分线。
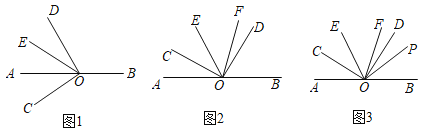
(1)如图1,若∠COE=63°,求∠BOD的度数;
(2)如图2,OF是∠B0C的平分线,求∠EOF的度数;
(3)如图3,在(2)的条件下,OP是∠BOD的一条三等分线,∠DOP=![]() ∠BOD,若∠AOC+∠DOF=∠EOF,求∠FOP的度数。
∠BOD,若∠AOC+∠DOF=∠EOF,求∠FOP的度数。
【答案】(1)∠BOD=126°;(2)∠EOF=45°;(3)∠FOP=35°
【解析】
(1)利用角平分线的性质即可解答
(2)令∠AOC=2α,得到∠BOD=90°-2α,利用角平分线的性质,得出∠BOF =90°-α,∠DOE =α+45°,即可解答
(3)根据题意由(2)得出α=15°,所以∠DOF=15°,∠BOD=60°,即可解答
(1)如图1,因为∠COD=90°,∠COE=63°
所以∠DOE=∠COD-∠COE=90°-63°=27°
因为OE是∠AOD的平分线
所以∠AOD=2∠D0E=54°
因为点O在直线AB上
所以∠BOD=180°-∠AOD=180°-54°=126°
(2)如图2,令∠AOC=2α
所以∠BOC=180°-∠AOC=180°-2α,∠AOD=∠AOC+∠COD=2a+90°
∠BOD=180°-∠AOD=180°-(2α+90°)=90°-2α
因为OE,OF分别是∠AOD,∠BOC的平分线
所以∠DOE=-∠AOD=α+45°,∠BOF=-∠BOC=90°-α
所以∠DOF=∠BOF-∠BOD=(90°-α)-(90°-2a)=α
所以∠EOF=∠DOE-∠DOF=(α+45°)-α=45°
(3)如图3,因为∠AOC+∠DOF=∠EOF
所以2α+α=45°,解得α=15°
所以∠DOF=15°,∠BOD=90°-30°=60°
所以∠DOP=![]() ∠BOD=20°
∠BOD=20°
所以∠FOP=∠DOF+∠DOP=15°+20°=35°
