题目内容
两条直线相交成四个角,如果其中一个角是90°,那么其它三个角各是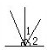
90
90
度,这两条直线叫做互相垂直
互相垂直
.右图中有5
5
条射线,2
2
个钝角.已知∠1=40°,∠2=50°
50°
.
分析:①两条直线相交,有两种情况:垂直或不垂直,如果其中一个角是90°,那么其它各个角都是90°,这两条直线相互垂直;②根据线段、直线、射线、锐角、直角、钝角的意义和特征,利用图形按一定的规律数出,求∠2的度数,用90度-∠1的度数即可.
解答:解:①两条直线相交,其中一个夹角为90°,那么这两条直线互相垂直;
②据图观察,图中有5条射线,2个钝角,已知∠1=40°,则∠2=90°-40°=50°;
故答案为:90,互相垂直,5,2,50°
②据图观察,图中有5条射线,2个钝角,已知∠1=40°,则∠2=90°-40°=50°;
故答案为:90,互相垂直,5,2,50°
点评:此题考查了互相垂直的含义及对射线和角的认识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目