题目内容
【题目】如图.长方形ABCD中,AB=12厘米,ED=DA=6厘米,小虫P从A出发,沿看长方形的边依次向B,C,D以每秒1厘米的速度移动.
(1)小虫P从A点出发几秒后,三角形APE是等腰直角三角形?
(2)当小虫P到达C时,另一只小虫Q以每秒2厘米的速度从A点出发.沿AB向B点移动,小虫Q从A点出发几秒后,四边形AQPE是梯形?

【答案】(1)12秒
(2)4秒
【解析】
(1)由图可知:当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;然后求出A点到B点的距离及A点到CD中点的距离,进而根据:路程÷速度=时间,分别解答即可;
(2)当DP∥AQ时,AQPE就是梯形,可设小虫Q从A点出发x秒后四边形AQPE是梯形,列式为12﹣x=2x,解答即可.
(1)如图:
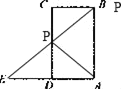
当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,
需要:12÷1=12(秒)
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,
需要:(12+6+6)÷1
=24÷1
=24(秒)
答:小虫P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形.
(2)如图:
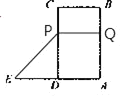
可设小虫Q从A点出发x秒后四边形AQPE是梯形,
12﹣x=2x
3x=12
x=4
答:小虫Q从A点出发4秒后,四边形AQPE是梯形.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
