题目内容
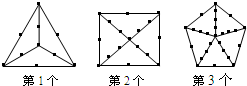 观察下列各图中小圆点的摆放规律,按这样的规律继续摆放下去,则第7个图形中小圆点的个数为
观察下列各图中小圆点的摆放规律,按这样的规律继续摆放下去,则第7个图形中小圆点的个数为82
82
.分析:根据题干可知,第1个图形中小圆点的个数为10个,可以写成10=(1+2)2+1;第2个图形中小圆点的个数为17个,可以写成17=(2+2)2+1;第3个图形中小圆点的个数为26个,可以写成26=(3+2)2+1;…由此第n个图形中的小圆点个数就可以写成:(n+2)2+1;由此即可解决问题.
解答:解:根据题意分析可得:第1个图形中小圆点的个数为:10=(1+2)2+1;
第2个图形中小圆点的个数为:17=(2+2)2+1;
第3个图形中小圆点的个数为:26=(3+2)2+1;
…
第n个图形中的小圆点的个数为:(n+2)2+1;
所以第7个图形中小圆点的个数为:(7+2)2+1,
=81+1,
=82(个);
答:第7个图形中小圆点的个数为82个.
故答案为:82.
第2个图形中小圆点的个数为:17=(2+2)2+1;
第3个图形中小圆点的个数为:26=(3+2)2+1;
…
第n个图形中的小圆点的个数为:(n+2)2+1;
所以第7个图形中小圆点的个数为:(7+2)2+1,
=81+1,
=82(个);
答:第7个图形中小圆点的个数为82个.
故答案为:82.
点评:本题是一道找规律的题目,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,并从已知的特殊个体推理得出一般规律.即可解决此类问题.

练习册系列答案
相关题目
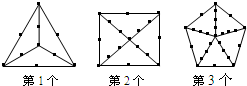 观察下列各图中小圆点的摆放规律,按这样的规律继续摆放下去,则第7个图形中小圆点的个数为________.
观察下列各图中小圆点的摆放规律,按这样的规律继续摆放下去,则第7个图形中小圆点的个数为________.