题目内容
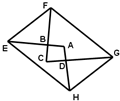如图，将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H，若四边形ABCD的面积为5，则四边形EFHG的面积为考点：组合图形的面积
专题：平面图形的认识与计算
分析：根据四边形ABCD的面积是5，要求四边形EFGH的面积，只要求出三角形EFB，三角形FCG，三角形GDH和三角形AEH四个三角形的面积之和再减去四边形ABCD的面积，即可解决问题
解答：
解：连接AC、BD、ED、EC、CH
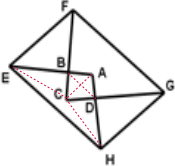
因的三角形ABC和三角形BCE的高相等，三角形BCE的底边是三角形ABC底边的2倍，所以三角形BCE的面积是三角形ABC面积的2倍．
因的三角形BEF和三角形BCE的高相等，三角形BEF的底边是三角形BCE底边的2倍，所以三角形BEF的面积是三角形BCE面积的2倍．
所以三角形BEF的面积是三角形ABC面积的4倍，
因的三角形ACD和三角形CDH的高相等，三角形CDH的底边是三角形ACD底边的2倍，所以三角形CDH的面积是三角形ACD面积的2倍．
因的三角形CDH和三角形DHG的高相等，三角形DHG的底边是三角形CDH底边的2倍，所以三角形DHG的面积是三角形CDH面积的2倍．
所以三角形DHG的面积是三角形ACD面积的4倍，
三角形ABD的三角形AEH底边的比是1：3，高的比也是1：3，所以三角形AEH的面积是三角形ABD面积的9倍，同理可证三角形CFG的面积是三角形BCD面积的9倍．
S△BEF+S△DHG+S△AEH+S△CFG
=4S△ABC+4S△ACD+9S△ABD+9S△BCD
=4（S△ABC+S△ACD）+9（S△ABD+S△BCD）
=4×5+9×5
=65（平方厘米）
S四边形EFGH=65-5=60（平方厘米）
答：四边形EFGH的面积是60平方厘米．
故答案为：60．
因的三角形ABC和三角形BCE的高相等，三角形BCE的底边是三角形ABC底边的2倍，所以三角形BCE的面积是三角形ABC面积的2倍．
因的三角形BEF和三角形BCE的高相等，三角形BEF的底边是三角形BCE底边的2倍，所以三角形BEF的面积是三角形BCE面积的2倍．
所以三角形BEF的面积是三角形ABC面积的4倍，
因的三角形ACD和三角形CDH的高相等，三角形CDH的底边是三角形ACD底边的2倍，所以三角形CDH的面积是三角形ACD面积的2倍．
因的三角形CDH和三角形DHG的高相等，三角形DHG的底边是三角形CDH底边的2倍，所以三角形DHG的面积是三角形CDH面积的2倍．
所以三角形DHG的面积是三角形ACD面积的4倍，
三角形ABD的三角形AEH底边的比是1：3，高的比也是1：3，所以三角形AEH的面积是三角形ABD面积的9倍，同理可证三角形CFG的面积是三角形BCD面积的9倍．
S△BEF+S△DHG+S△AEH+S△CFG
=4S△ABC+4S△ACD+9S△ABD+9S△BCD
=4（S△ABC+S△ACD）+9（S△ABD+S△BCD）
=4×5+9×5
=65（平方厘米）
S四边形EFGH=65-5=60（平方厘米）
答：四边形EFGH的面积是60平方厘米．
故答案为：60．
点评：解答此题的关键是，根据题意，添加辅助线，利用三角形的面积公式，帮助我们找到三角形之间的关系，由此即可解答．
练习册系列答案
相关题目
