题目内容
 小明和小兰分别从相距40千米的A、B两地同时出发,相向而行,经过4小时相距4千米,再经过1小时,小明到B地的路程是小兰到A地的路程的2倍,请分别求出小明和小兰的速度.
小明和小兰分别从相距40千米的A、B两地同时出发,相向而行,经过4小时相距4千米,再经过1小时,小明到B地的路程是小兰到A地的路程的2倍,请分别求出小明和小兰的速度.
解:(1)相遇前相距4千米,小明和小兰的速度之和为:
(40-4)÷4,
=36÷4,
=9(千米);
设小明的速度为每小时x千米,则小兰的速度为每小时9-x千米,得:
40-5x=2×[40-5(9-x)]
40-5x=80-90+10x
15x=50
x= ;
;
则9-x=9- =
=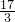 .
.
答:小明的速度为每小时 千米,则小兰的速度为每小时
千米,则小兰的速度为每小时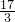 千米.
千米.
(2)相遇后两人的距离为4千米:
小明和小兰的速度之和为:
(40+4)÷4,
=44÷4,
=11(千米);
设小明的速度为每小时x千米,则小兰的速度为每小时(11-x)千米,得:
40-5x=2×[40-5(11-x)],
40-5x=80-110+10x
15x=70
x=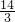 ;
;
则11-x=11-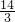 =
=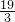 (千米).
(千米).
答:小明的速度为每小时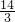 千米,则小兰的速度为每小时
千米,则小兰的速度为每小时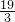 千米.
千米.
分析:此题分两种情况:(1)如果相遇前相距4千米,则小明和小兰的速度之和为:(40-4)÷4=9(千米).
设小明的速度为每小时x千米,则小兰的速度为每小时(9-x)千米,由题意得:40-5x=2×[40-5(9-x)],解方程即可;
(2)如果是相遇后,两人的距离为4千米,则小明和小兰的速度之和为:(40+4)÷4=11(千米)
设小明的速度为每小时x千米,则小兰的速度为每小时(11-x)千米,由题意得:40-5x=2×[40-5(11-x)],解方程即可.
点评:此题解答的关键是分为两种情况,那就是相遇前相距4千米,或相遇后两人的距离为4千米.
(40-4)÷4,
=36÷4,
=9(千米);
设小明的速度为每小时x千米,则小兰的速度为每小时9-x千米,得:
40-5x=2×[40-5(9-x)]
40-5x=80-90+10x
15x=50
x=
 ;
;则9-x=9-
 =
=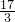 .
.答:小明的速度为每小时
 千米,则小兰的速度为每小时
千米,则小兰的速度为每小时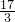 千米.
千米.(2)相遇后两人的距离为4千米:
小明和小兰的速度之和为:
(40+4)÷4,
=44÷4,
=11(千米);
设小明的速度为每小时x千米,则小兰的速度为每小时(11-x)千米,得:
40-5x=2×[40-5(11-x)],
40-5x=80-110+10x
15x=70
x=
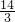 ;
;则11-x=11-
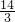 =
=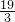 (千米).
(千米).答:小明的速度为每小时
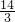 千米,则小兰的速度为每小时
千米,则小兰的速度为每小时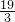 千米.
千米.分析:此题分两种情况:(1)如果相遇前相距4千米,则小明和小兰的速度之和为:(40-4)÷4=9(千米).
设小明的速度为每小时x千米,则小兰的速度为每小时(9-x)千米,由题意得:40-5x=2×[40-5(9-x)],解方程即可;
(2)如果是相遇后,两人的距离为4千米,则小明和小兰的速度之和为:(40+4)÷4=11(千米)
设小明的速度为每小时x千米,则小兰的速度为每小时(11-x)千米,由题意得:40-5x=2×[40-5(11-x)],解方程即可.
点评:此题解答的关键是分为两种情况,那就是相遇前相距4千米,或相遇后两人的距离为4千米.

练习册系列答案
相关题目
 小明和小兰分别从相距40千米的A、B两地同时出发,相向而行,经过4小时相距4千米,再经过1小时,小明到B地的路程是小兰到A地的路程的2倍,请分别求出小明和小兰的速度.
小明和小兰分别从相距40千米的A、B两地同时出发,相向而行,经过4小时相距4千米,再经过1小时,小明到B地的路程是小兰到A地的路程的2倍,请分别求出小明和小兰的速度.