题目内容
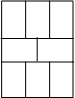
如图,由8个同样的小长方形拼成一个大长方形.大长方形的周长是84厘米.大长方形的面积是________平方厘米.
588
分析:从上面三个小长方形和中间的两个小长方形的排列可以看出:在小长方形中,2长=3宽.则大长方形的周长=(4宽+2长)×2,把2长=3宽代入,可得宽,进而可求大长方形的长(小长方形的3宽)和宽(小长方形的2长+宽=4宽),长乘宽可得面积.
解答:在小长方形中,2长=3宽,所以:
84=(4宽+2长)×2,
84=7宽×2,
84=14宽,
宽=7(厘米).
大长方形的宽为:7×3=21(厘米),
大长方形的长为:7×4=28(厘米),
大长方形的面积为:21×28=588(平方厘米).
故答案为:588.
点评:观察图形,根据图形中小长方形的排列可得小长方形中长与宽的关系,结合已知可求得宽,进而求解.
分析:从上面三个小长方形和中间的两个小长方形的排列可以看出:在小长方形中,2长=3宽.则大长方形的周长=(4宽+2长)×2,把2长=3宽代入,可得宽,进而可求大长方形的长(小长方形的3宽)和宽(小长方形的2长+宽=4宽),长乘宽可得面积.
解答:在小长方形中,2长=3宽,所以:
84=(4宽+2长)×2,
84=7宽×2,
84=14宽,
宽=7(厘米).
大长方形的宽为:7×3=21(厘米),
大长方形的长为:7×4=28(厘米),
大长方形的面积为:21×28=588(平方厘米).
故答案为:588.
点评:观察图形,根据图形中小长方形的排列可得小长方形中长与宽的关系,结合已知可求得宽,进而求解.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目