Question

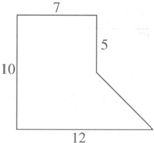用多种方法求下列组合图形的面积．（单位：cm）

Answer 1

解：方法一：10×7+（12-7）×5÷2，
=70+12.5，
=82.5（平方厘米）；
方法二：7×5+（7+12）×（10-5）÷2，
=35+19×5÷2，
=35+47.5，
=82.5（平方厘米）；
方法三：12×10-（5+10）×（12-7）÷2，
=120-15×5÷2，
=120-37.5，
=82.5（平方厘米）；
答：这个图形的面积是82.5平方厘米．
分析：如图，这个图形的面积等于长10厘米、宽7厘米的长方形与直角边长都是5厘米的直角三角形的面积之和，也等于长7厘米，宽5厘米的长方形与上底7厘米、下底12厘米、高5厘米的梯形的面积之和；也等于长12厘米、宽10厘米的长方形与上底5厘米、下底10厘米、高12-7=5厘米的梯形的面积之差，据此计算即可解答．

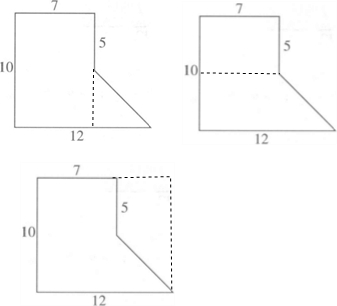
点评：此题考查了利用割补法，计算组合图形的面积的计算方法．